Предмет: Геометрия,
автор: Извращуга1801
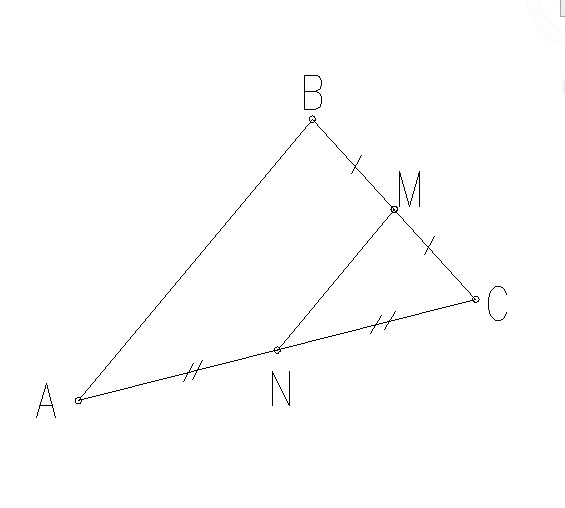
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 20. Найдите площадь четырёхугольника ABMN.
Ответы
Автор ответа:
0
Отношение площадей 2 подобных треугольников равно квадрату коэффициента подобия.
обозначу площадь треугольника АВС - S1, а треугольника CMN - S2, а коэффициент подобия - к
итого S1/S2=к²
S1=S2*к²
к²=(СВ/СМ)² СВ=2СМ
к²=(2СМ/СМ)²=2²=4
S1=4*20=80
S четырёхугольника=80-20=60
обозначу площадь треугольника АВС - S1, а треугольника CMN - S2, а коэффициент подобия - к
итого S1/S2=к²
S1=S2*к²
к²=(СВ/СМ)² СВ=2СМ
к²=(2СМ/СМ)²=2²=4
S1=4*20=80
S четырёхугольника=80-20=60
Приложения:
Похожие вопросы
Предмет: Математика,
автор: tanyapoprygunchik
Предмет: Математика,
автор: Viktoria12264
Предмет: Биология,
автор: devochka0899
Предмет: Геометрия,
автор: ldarenkova