Предмет: Математика,
автор: olmuza
Помогите пожалуйста решить экстремумы !!!!!! Срочно
Приложения:
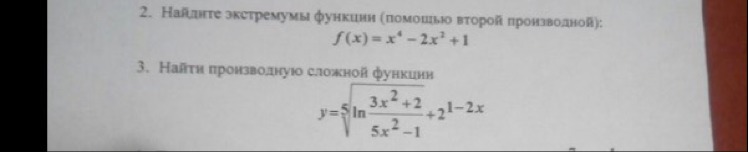
Ответы
Автор ответа:
0
Задача: найти локальные экстремумы функции  .
.
Воспользуемся вторым достаточным условием экстремума: если и
и  , то точка
, то точка  является точкой экстремума, причём если
является точкой экстремума, причём если  , то т.
, то т.  является точкой локального минимума, а если
является точкой локального минимума, а если  , то точкой максимума.
, то точкой максимума.
1. Найдём точки, подозрительные на экстремум из условия .
.


Таким образом, точками, подозрительными на экстремум, являются точки
2. Определим характер данных точек экстремума. Для этого вычислим вторую производную и подсчитаем её значения в данных точках.

 т.
т.  является точкой локального максимума. Поэтому значение
является точкой локального максимума. Поэтому значение  является локальным максимумом функции
является локальным максимумом функции  .
.
 т.
т.  является точкой локального минимума. Поэтому значение
является точкой локального минимума. Поэтому значение  является локальным минимумом функции
является локальным минимумом функции  .
.
 т.
т.  является точкой локального максимума. Поэтому значение
является точкой локального максимума. Поэтому значение  является локальным минимумом функции
является локальным минимумом функции  .
.
P.S. - Прилагаю картинку со скриншотом решения, т.к. у автора вопроса почему-то некорректно отображаются формулы.
Воспользуемся вторым достаточным условием экстремума: если
1. Найдём точки, подозрительные на экстремум из условия
Таким образом, точками, подозрительными на экстремум, являются точки
2. Определим характер данных точек экстремума. Для этого вычислим вторую производную и подсчитаем её значения в данных точках.
P.S. - Прилагаю картинку со скриншотом решения, т.к. у автора вопроса почему-то некорректно отображаются формулы.
Приложения:

Автор ответа:
0
Что написано в квадратных скобках ?
Автор ответа:
0
Квадратные скобки - это совокупность. Читается как "выполнено А или Б".
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: jgvhvgjhugjjgvhv
Предмет: Математика,
автор: zhannasivtseva
Предмет: Математика,
автор: polianskaia