Question

При каком значении параметра b система уравнений x^2+y=b; x^2+y^2=5 имеет: а) одно решение; б) три решения?

Answer 1

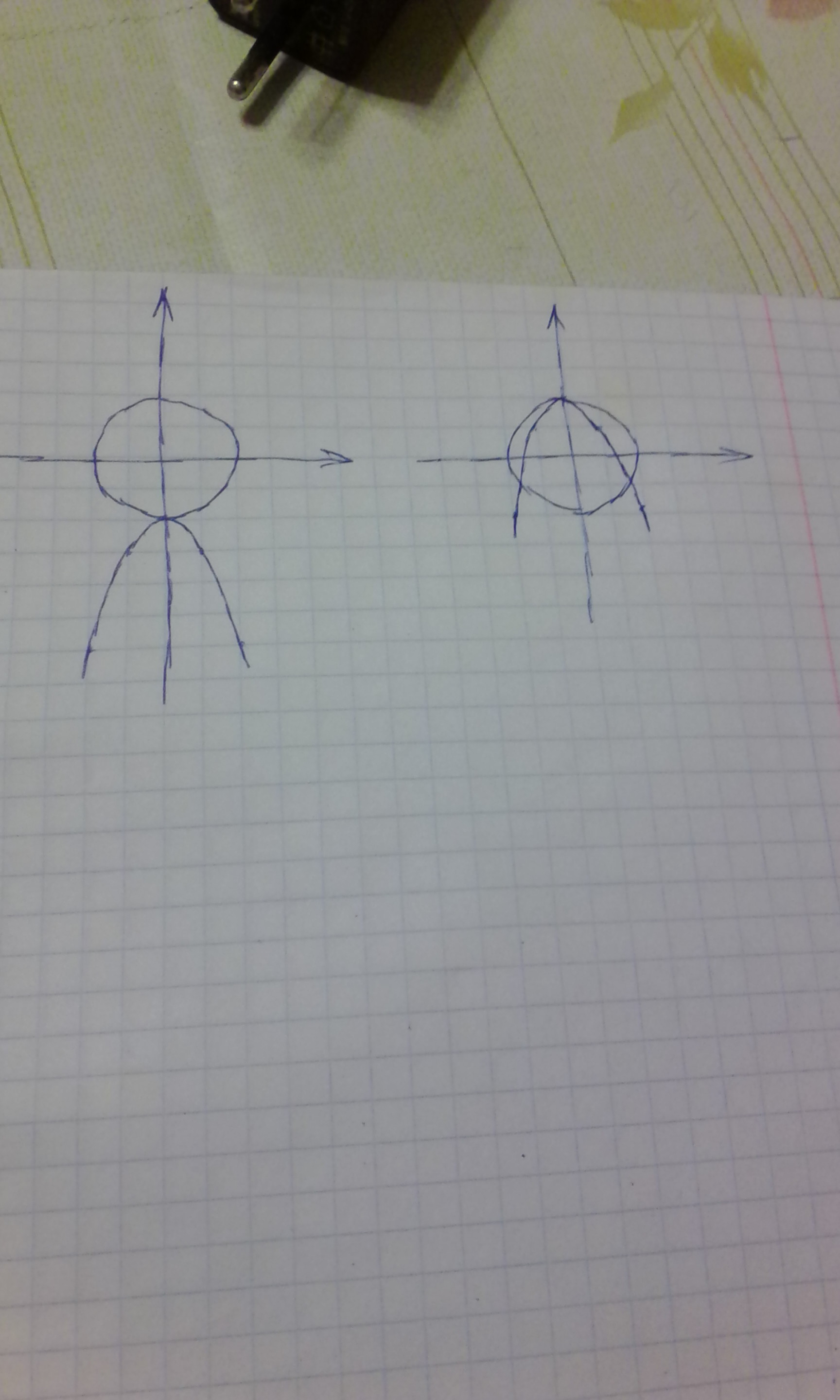
Уравнение x^2+y=b это парабола с ветвями вниз:
y=-x^2+b.
Она имеет вершину в точке А(0,b)
Уравнение x^2+y^2=5 это окружность с центром О(0;0) и радиусом R=√5.
А) Они пересекаются в 1 точке, когда парабола касается окружности снизу.
A1(0; -√5); b=-√5.
Б) Они пересекаются в 3 точках, когда парабола касается вершиной верхней точки окружности.
A2(0; √5); b=√5.
Оба случая показаны на рисунке.