Предмет: Математика,
автор: honr
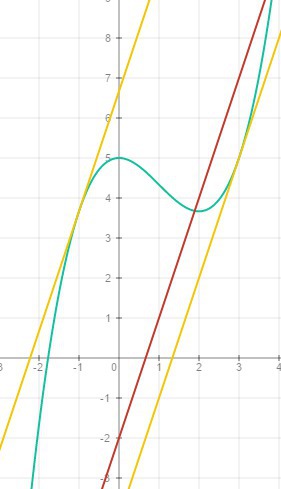
написать уравнение той касательной к графику функции у=1/3x^3-х^2+5 которая паралельно прямой у=3x-2
Ответы
Автор ответа:
0
f(x)=1/3x³-х²+5;
у=3x-2, k=3.
У параллельных прямых коэффициенты при х равные, т.е. k=3.
Уравнение касательной можно найти по формуле:
y=f(x0)+f'(x0)(x-x0).
Найдем производную функции:
f'(x)=(1/3x³-х²+5)'=x²-2x=3=k.
x²-2x-3=0;
D=16;
x1=-1; x2=3.
Это значит, что таких касательных будет две.
Найдем уравнения этих касательных:
1) f(-1)=3 2/3; f'(-1)=3;
y=3 2/3+3(x+1)=3x+6 2/3.
y=3x+6 2/3.
2) f(3)=5; f'(3)=3;
y=5+3(x+3)=3x-4.
y=3x-4.
у=3x-2, k=3.
У параллельных прямых коэффициенты при х равные, т.е. k=3.
Уравнение касательной можно найти по формуле:
y=f(x0)+f'(x0)(x-x0).
Найдем производную функции:
f'(x)=(1/3x³-х²+5)'=x²-2x=3=k.
x²-2x-3=0;
D=16;
x1=-1; x2=3.
Это значит, что таких касательных будет две.
Найдем уравнения этих касательных:
1) f(-1)=3 2/3; f'(-1)=3;
y=3 2/3+3(x+1)=3x+6 2/3.
y=3x+6 2/3.
2) f(3)=5; f'(3)=3;
y=5+3(x+3)=3x-4.
y=3x-4.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: bilejludmila154
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: vladashevsenko
Предмет: Литература,
автор: lera34555
Предмет: Математика,
автор: losharikssss