Предмет: Геометрия,
автор: Solнышко
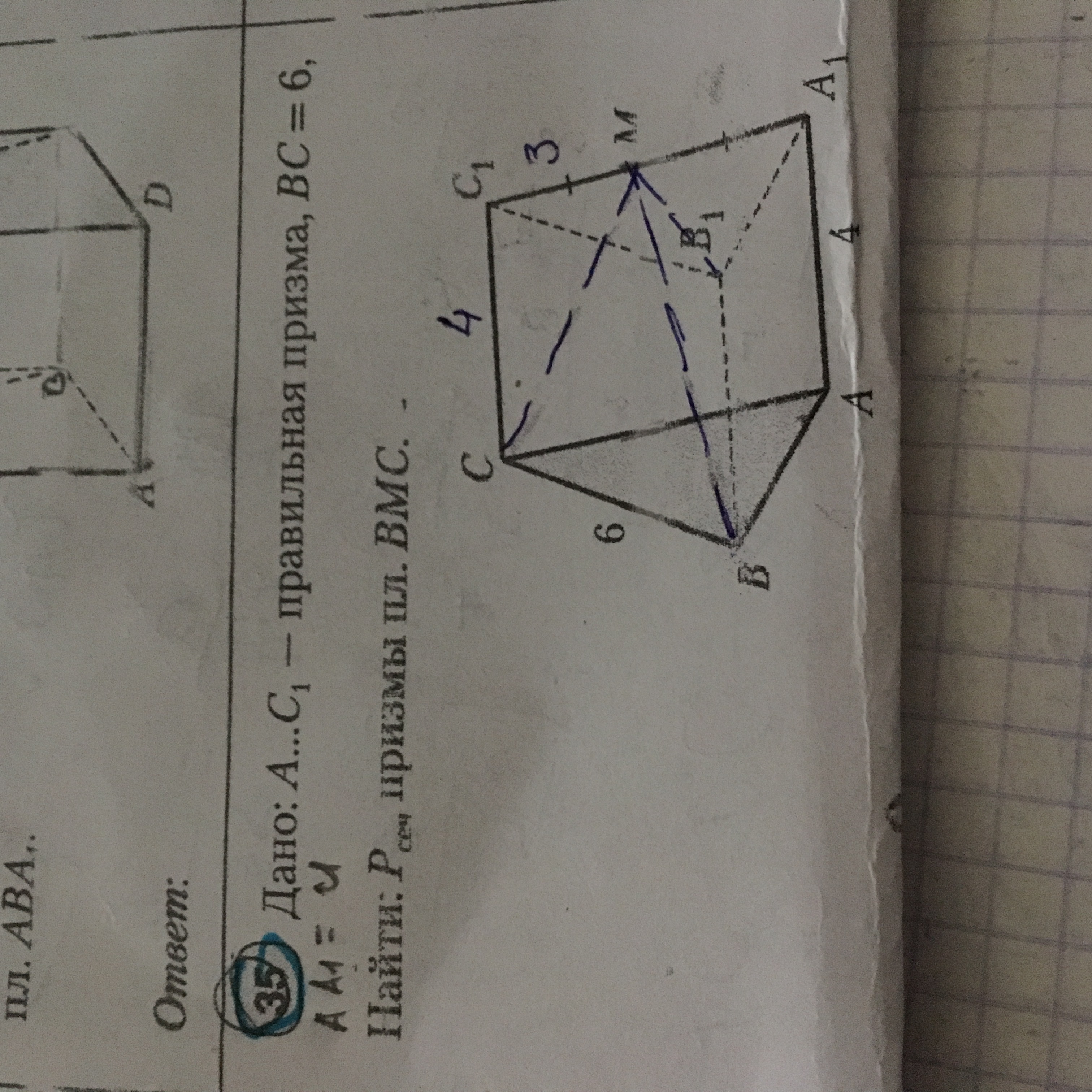
АВСДА1В1С1Д1 - правильная призма. Точка М делит сторону А1С1 на равные части. СС1 = 4 . А1С1 = 6. Найдите периметр сечения призмы плоскостью ВМС.
Я решила, но с ответом не сходится. Помогите пожалуйста. ))))))))))))))
Приложения:
Ответы
Автор ответа:
0
АВСДА1В1С1Д1 - правильная призма. Точка М делит сторону А1С1 на равные части. СС1 = 4 . А1С1 = 6. Найдите периметр сечения призмы плоскостью ВМС.
Решение: Плоскость ВМС отсекает в правильной призме равнобедренную усеченную трапецию BMKC. Причем точка находится на середине ребра В1А1.
Длина отрезка МК(верхнее основание трапеции) как средней линии треугольника А1В1С1 равна половине длины В1С1
МК =В1С1/2 =6/2=3
Дина нижнего основания трапеции равна ВС=6
Боковые стороны CМ и BК равны и найходятся по тереме Пифагора из треугольника СС1М

Определим высоту трапеции

Находим площадь трапеции по формуле

Решение: Плоскость ВМС отсекает в правильной призме равнобедренную усеченную трапецию BMKC. Причем точка находится на середине ребра В1А1.
Длина отрезка МК(верхнее основание трапеции) как средней линии треугольника А1В1С1 равна половине длины В1С1
МК =В1С1/2 =6/2=3
Дина нижнего основания трапеции равна ВС=6
Боковые стороны CМ и BК равны и найходятся по тереме Пифагора из треугольника СС1М
Определим высоту трапеции
Находим площадь трапеции по формуле
Автор ответа:
0
ответ не верный. Я вчера решила сама.
Похожие вопросы
Предмет: Информатика,
автор: elizavetapodnebesnaa
Предмет: Психология,
автор: marinasuslina222
Предмет: Қазақ тiлi,
автор: dauletratbek91
Предмет: Математика,
автор: gaziz198150
Предмет: Обществознание,
автор: Лера9814