Предмет: Алгебра,
автор: adimas1
Пишите максимально подробное решение, кто правильно решит и подробно, тому лучшего
Приложения:
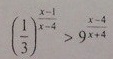
Ответы
Автор ответа:
0
ОДЗ x≠4 U x≠-4
(3^-1)^[(x-1)/(x-4)]>3^[(2x-8)/(x-4)]
(1-x)/(x-4)>(2x-8)/(x+4)
(2x-8)/(x+4)+(x-1)/(x-4)<0
(2x²-8x-8x+32+x²-x+4x-4)/(x+4)(x-4)<0
(3x²-13x+28)/(x-4)(x+4)<0
3x²-13x+28=0
D=169-336=-167⇒выражение больше 0 при любом х⇒
(x+4)(x-4)<0
x=-4 x=4
+ _ +
-------------(-4)---------------(4)------------
x∈(-4;4)
(3^-1)^[(x-1)/(x-4)]>3^[(2x-8)/(x-4)]
(1-x)/(x-4)>(2x-8)/(x+4)
(2x-8)/(x+4)+(x-1)/(x-4)<0
(2x²-8x-8x+32+x²-x+4x-4)/(x+4)(x-4)<0
(3x²-13x+28)/(x-4)(x+4)<0
3x²-13x+28=0
D=169-336=-167⇒выражение больше 0 при любом х⇒
(x+4)(x-4)<0
x=-4 x=4
+ _ +
-------------(-4)---------------(4)------------
x∈(-4;4)
Автор ответа:
0
3^[(x-4)/(x-1)]>3^[(2x-8)/(x-4)]
(x-4)/(x-1)>(2x-8)/(x+4)
(x-4)/(x-1)>(2x-8)/(x+4)
Автор ответа:
0
Здесь знак неравенства не должен измениться?
Автор ответа:
0
На <
Автор ответа:
0
основание больше 1,знак не меняется
Автор ответа:
0
3^[(x-4)/(x-1)]>3^[(2x-8)/(x-4)] Справа знаменатель знак + а не минус))
Похожие вопросы
Предмет: Математика,
автор: jaydz
Предмет: Математика,
автор: ermolin357
Предмет: Алгебра,
автор: meeeeeeeeeeeeeee
Предмет: История,
автор: 89052913444a