Предмет: Алгебра,
автор: asfasgfyh
до завтра помогите
пожалуйста
Приложения:
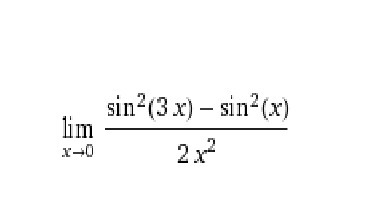
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: karina21072008
Предмет: Английский язык,
автор: 0956848
Предмет: Қазақ тiлi,
автор: tresher56
Предмет: Алгебра,
автор: Сашенькa666
Предмет: Обществознание,
автор: zudrilova