Question

Исследовать на направление выпуклости- вогнутости и найти точки перегиба у=x^4-6x^2+5

Answer 1

ДАНО
Y = x⁴ - 6x² + 5
Для этого используем только производные.
ПЕРВАЯ производная - точки экстремумов
Y' = 4x³-12x = 4x*(x²-3)
х1 = 0 и х2= -√3 и х3 = +√3
ВТОРАЯ производная - точки перегиба
Y' = 12x² - 12 = 12*(x²-1) = 12*(x-1)(x+1)
х4 = -1 и х5 = +1.
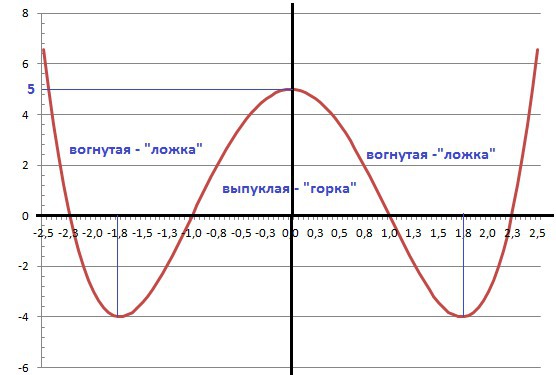
И для наглядности график - просто прелесть.
Вогнутая - Х∈(-∞; -1]∪[1;+∞)
Выпуклая - Х∈[-1;1]

Answer 2

3-ю, 4-ю и 5-ю строчки можно написать только после того ,как будет проведено исследование на выпуклость и вогнутость. 1. определены знаки второй производной на промежутках, на которые критические точки второго рода разбивают всю область определения функции. и можно строить график функции "для наглядности"