Предмет: Геометрия,
автор: sakasasarasasa
В трапеции авсд известно что вс параллельно ад, ав перпендикулярно ад, ВС равно СД, угол АВД равен 80 градусов. Найдите углы трапеции.
Ответы
Автор ответа:
0
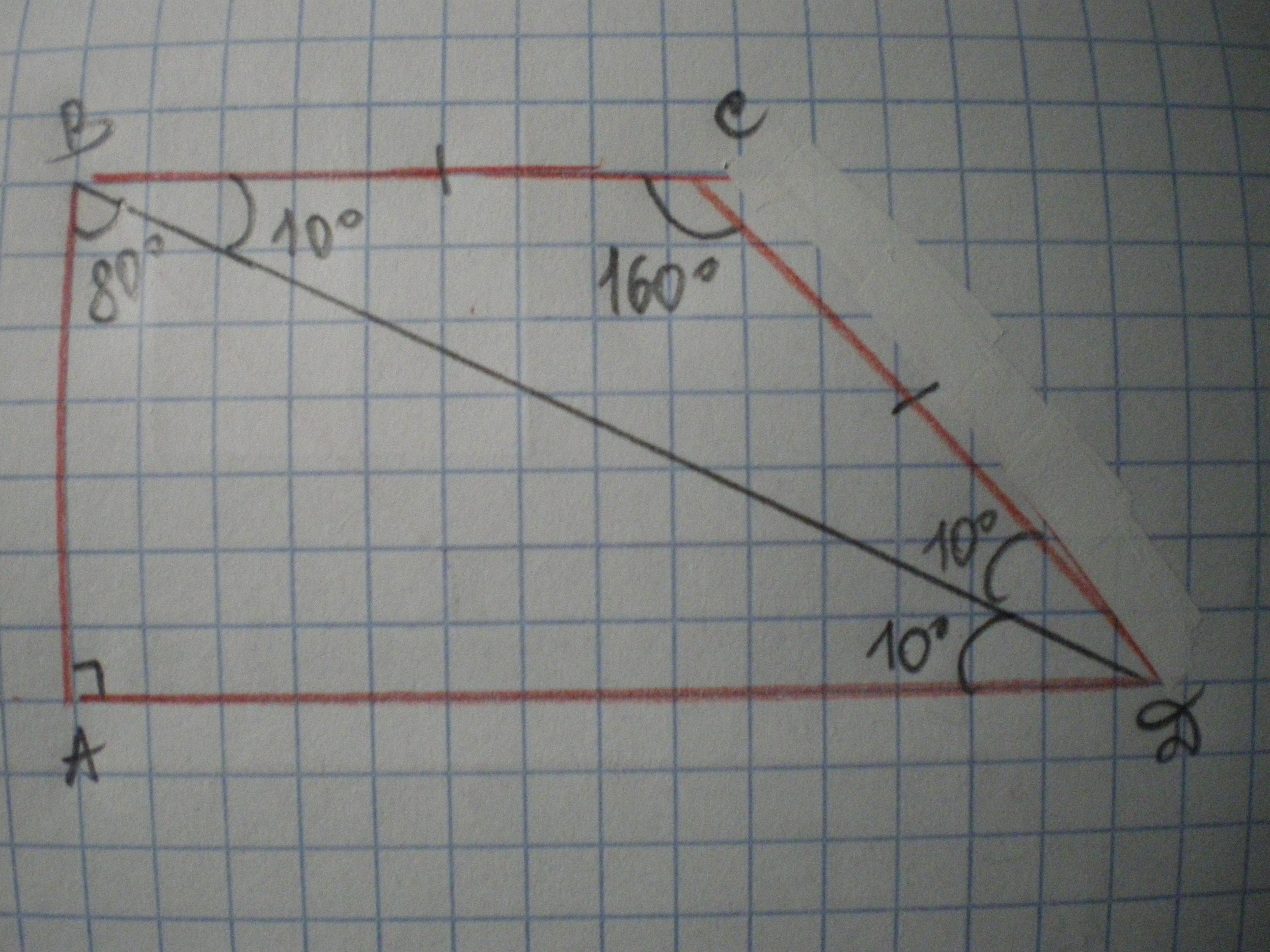
Дано: АВСD - трапеция, AD║BC, AB⊥AD, BC=CD, ∠ABD=80°. Найти ∠А, ∠В, ∠С, ∠D.
1 способ. Рассмотрим ΔАВD - прямоугольный (по условию), ∠ABD=80°, значит ∠BDА=90-80=10° по свойству суммы острых углов прямоугольного треугольника.
∠АВС=90°, т.к. AB⊥AD и AD║BC, поэтому ∠CBD=90-80=10°.
ΔВСD - равнобедренный, т.к. BC=CD, значит, ∠CBD=∠CDВ=10°
∠D=10+10=20°
∠С=180-20=160°
2 способ. ΔАВD - прямоугольный, ∠А=90° по условию, ∠АВD+∠ADB=90° т.к. сумма острых углов прямоугольного треугольника составляет 90°; ∠ADB=90-80=10°
∠DBC=∠ADB=10° как внутренние накрест лежащие при AD║BC и секущей BD.
∠В=80+10=90°; ∠D=10+10=20°
CD=ВС по условию, значит ΔВСD - равнобедренный и ∠СDВ=∠DBC=10°;
∠C=180-20=160°
Ответ: 90°, 90°, 160°, 20°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: yumornoi3321
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: Notv
Предмет: Математика,
автор: dinar4ik890890