Предмет: Алгебра,
автор: sveta3760
решите пожалуйста...даю 25 баллов
Приложения:
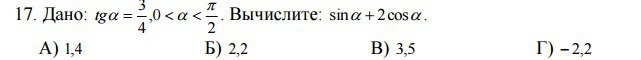
Ответы
Автор ответа:
0
Дано tgα=3/4, 0<α<π/2. Найти sinα+2cosα.
Решение. В заданной области угла 0<α<π/2 значения sinα и cosα положительные.
Определим значение cosα по формуле


Значение sinα найдем по формуле
sinα =cosα*tgα =
Окончательно получим

Решение. В заданной области угла 0<α<π/2 значения sinα и cosα положительные.
Определим значение cosα по формуле
Значение sinα найдем по формуле
sinα =cosα*tgα =
Окончательно получим
Автор ответа:
0
и какой ответ
Автор ответа:
0
Правильный ответ Б 2,2
Автор ответа:
0
спасибо
Похожие вопросы
Предмет: Право,
автор: vladikrealme
Предмет: Русский язык,
автор: sinyakovada
Предмет: Литература,
автор: odessaroma098
Предмет: Математика,
автор: vlad1b2ovladdd