Question

f(x) = 6 - √(7-6x-x²)
Нужно найти E(f)

Answer 1

Берём производную функции, чтобы определить критические точки:
f'(x) = (6 - √(7-6x-x²))'=-1/2√7-6x-x²*(-6-2x)=(3+x)/√7-6x-x².
Находим критические точки, приравнивая производную к нулю:
(3+x)/√7-6x-x²=0;
3+x=0;
x=-3.
7-6x-x²>0;
D=64;
x1=-7, x2=1.
x∈(-7; 1).
Находим значения функции в этих точках:
f(-7)=6 - max;
f(1)=6 - max;
f(-3)=2 - min.
Получаем, что Е=[2; 6].
Ответ: Е=[2; 6].
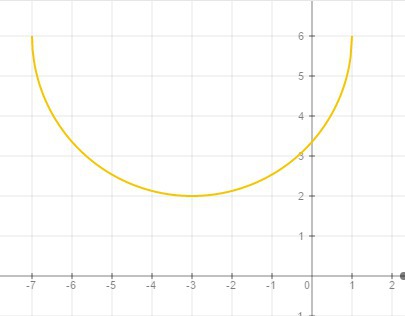
Это можно увидеть и на графике функции.