Question

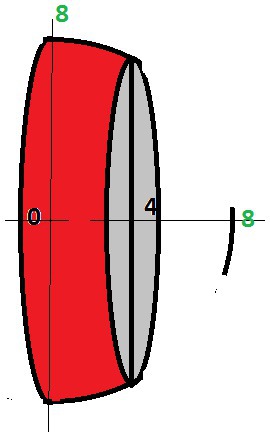
вычислить объем (V) тела, ограниченного плоскостью x=b и поверхностью, образованной вращением вокруг оси OX графика заданной функции y=√(64-x^2), [0,4]

Answer 1

объем тела вычисляется интегрированием по формуле
$V= pi intlimits^4_0 { (64-x^2)} , dx = frac{704}{3}* pi$
Пределы интегрирования от 0 до 4.
ОТВЕТ 234 2/3*π
А функция -  это обрезанный шар радиусом 8.

Answer 2

Площадь круга на удалении x от нуля равна S(x)=пy²(x), а дифференциал объёма: dV = пy²dx = п(64-x²) dx, интегрируем и получаем:
п ∫ (64-x²) dx = п ∫ 64 dx – п ∫ x²dx = 64пx – пx³/3 + C = (пx/3)( 192 – x² ) + C ;
V = п ∫ (64-x²) dx |[0,4] = (пx/3)( 192 – x² ) |[0,4] = (4п/3)( 192 – 4² ) = (4п/3)( 192 – 16 ) = 704п/3 .