Предмет: Алгебра,
автор: grungfun
Найдите пожалуйста неопределенный интеграл
Приложения:
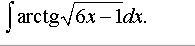
Ответы
Автор ответа:
0
Для начала делаем замену:

Получаем такой интеграл:
Берем его по частям:

Теперь обратная замена и ответ:

Получаем такой интеграл:
Берем его по частям:
Теперь обратная замена и ответ:
Похожие вопросы
Предмет: Физика,
автор: fuglygirll
Предмет: Математика,
автор: pupsiklex
Предмет: Геометрия,
автор: Zere9875
Предмет: Математика,
автор: Аноним