Предмет: Математика,
автор: УмнаяТагиева
Пожалуйста решите Уравнение.
Приложения:
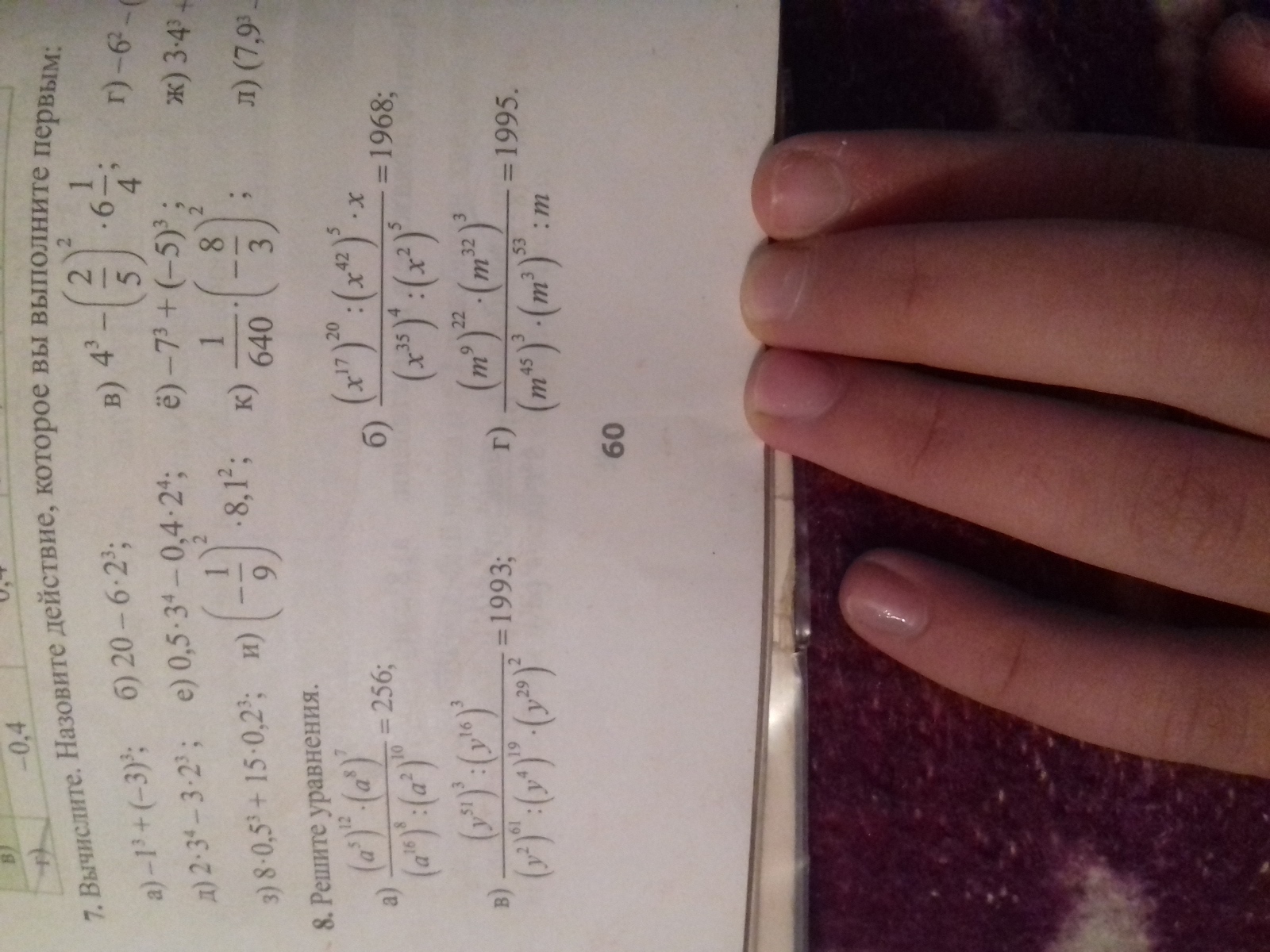
Ответы
Автор ответа:
0
а) 
Сначала упростим выражение в левой части уравнения (можно записать его отдельно и упрощать, но я этот пример буду писать полностью, каждый раз переписывая всё уравнение).
При возведении степени в степень- показатели перемножаются:


При перемножении степеней с одинаковыми основаниями- показатели складываются (а при делении- вычитаются):


Применяем то же самое правило, что и выше:



Показатель степени (восемь)- чётное число, поэтому появился второй корень (минус два), ведь отрицательное число при возведении в чётную степень даёт положительное число.
При проверке в исходном уравнении, этот корень туда подходит (так как все множители/делители в исходной дроби содержат чётные показатели степени, значит в результате всегда получится положительное число).
б)
Теперь будем решать по тем же правилам, но преобразовывая отдельно левую часть уравнения (как у вас принято записывать, тот вариант и выбирай).

Теперь запишем наше исходное уравнение, но с уже упрощённой левой частью:
 (мы сразу получили ответ, то есть нашли корень уравнения)
(мы сразу получили ответ, то есть нашли корень уравнения)
в)
Будем решать по тем же правилам (упрощая отдельно левую часть), но не расписывать так подробно, будем упрощать ещё быстрее:

Теперь запишем наше исходное уравнение, но с уже упрощённой левой частью:
 (мы опять сразу же получили ответ)
(мы опять сразу же получили ответ)
г)
Будем упрощать левую часть по тем же правилам, но ещё быстрее, чем в последнем примере (сразу будем считать все показатели степени):

Теперь запишем наше исходное уравнение, но с уже упрощённой левой частью:

Сначала упростим выражение в левой части уравнения (можно записать его отдельно и упрощать, но я этот пример буду писать полностью, каждый раз переписывая всё уравнение).
При возведении степени в степень- показатели перемножаются:
При перемножении степеней с одинаковыми основаниями- показатели складываются (а при делении- вычитаются):
Применяем то же самое правило, что и выше:
Показатель степени (восемь)- чётное число, поэтому появился второй корень (минус два), ведь отрицательное число при возведении в чётную степень даёт положительное число.
При проверке в исходном уравнении, этот корень туда подходит (так как все множители/делители в исходной дроби содержат чётные показатели степени, значит в результате всегда получится положительное число).
б)
Теперь будем решать по тем же правилам, но преобразовывая отдельно левую часть уравнения (как у вас принято записывать, тот вариант и выбирай).
Теперь запишем наше исходное уравнение, но с уже упрощённой левой частью:
в)
Будем решать по тем же правилам (упрощая отдельно левую часть), но не расписывать так подробно, будем упрощать ещё быстрее:
Теперь запишем наше исходное уравнение, но с уже упрощённой левой частью:
г)
Будем упрощать левую часть по тем же правилам, но ещё быстрее, чем в последнем примере (сразу будем считать все показатели степени):
Теперь запишем наше исходное уравнение, но с уже упрощённой левой частью:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: zemlykkate8
Предмет: Биология,
автор: missLu
Предмет: Математика,
автор: gulnozaakm