Question

Найдите радиус окружности, описанной около равнобедренной трапеции, учитывая, что ее: а)большие и меньшие основания и высота соответственно равны 11,5 и 4
Даю максимум баллов

Answer 1

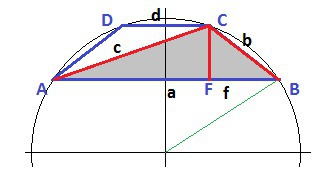
Делаем чертеж и обозначаем нужные стороны.
1. Радиус описанной окружности вокруг треугольника АВС -
$R= frac{abc}{4 sqrt{p(p-a)(p-b)(p-c)} }$
где р = (a+b+c)/2.
a = 11 - дано.
f = (a-d)2 = (11-5)2 = 3
CF= 4 - дано.
По т. Пифагора 
b = 5 ("египетский треугольник" 3:4:5)
AF = a -f = 11 - 3 = 8.
По т. Пифагора
с = √(8²+4²) = √80 = 4√5.
Полупериметр треугольника
p = (11+5+4√5)/2 = 8+4√5.~12.47
Подставили значения в формулу радиуса и получили под корнем 484
R = 5.59 см - ОТВЕТ
  

Answer 2

почему b=5, если AD+BC=AB+CD=11+5=16, a AD=BC?