Предмет: Алгебра,
автор: yatvoydroug
Логарифмическое неравенство
Заранее огромное спасибо!
Приложения:
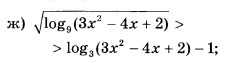
Ответы
Автор ответа:
0
Сразу напрашивается замена  . Тогда
. Тогда

Если t<1 неравенство выполняется при любом t≥0. Значит часть решения выглядит так: 0≤t<1
Если t≥1 мы имеем право возвести обе части в квадрат:

Объединим оба полученных промежутка и получим 0≤t<2. Возвращаемся к замене:

Решаем и получаем ответ: (-1; 1/3] U [1; 7/3)
Если t<1 неравенство выполняется при любом t≥0. Значит часть решения выглядит так: 0≤t<1
Если t≥1 мы имеем право возвести обе части в квадрат:
Объединим оба полученных промежутка и получим 0≤t<2. Возвращаемся к замене:
Решаем и получаем ответ: (-1; 1/3] U [1; 7/3)
Автор ответа:
0
Спасибо Вам большое!!!
Похожие вопросы
Предмет: Обществознание,
автор: romanfahrutdinov1
Предмет: Математика,
автор: pacan2075446
Предмет: Математика,
автор: symbattolegen07
Предмет: Геометрия,
автор: naumovalexxxei