Question

Помогите пожалуйста с геометрией
в кубе ABCDA1B1C1D1 найдите тангенс угла между плоскостями ABC и CB1D1

Answer 1

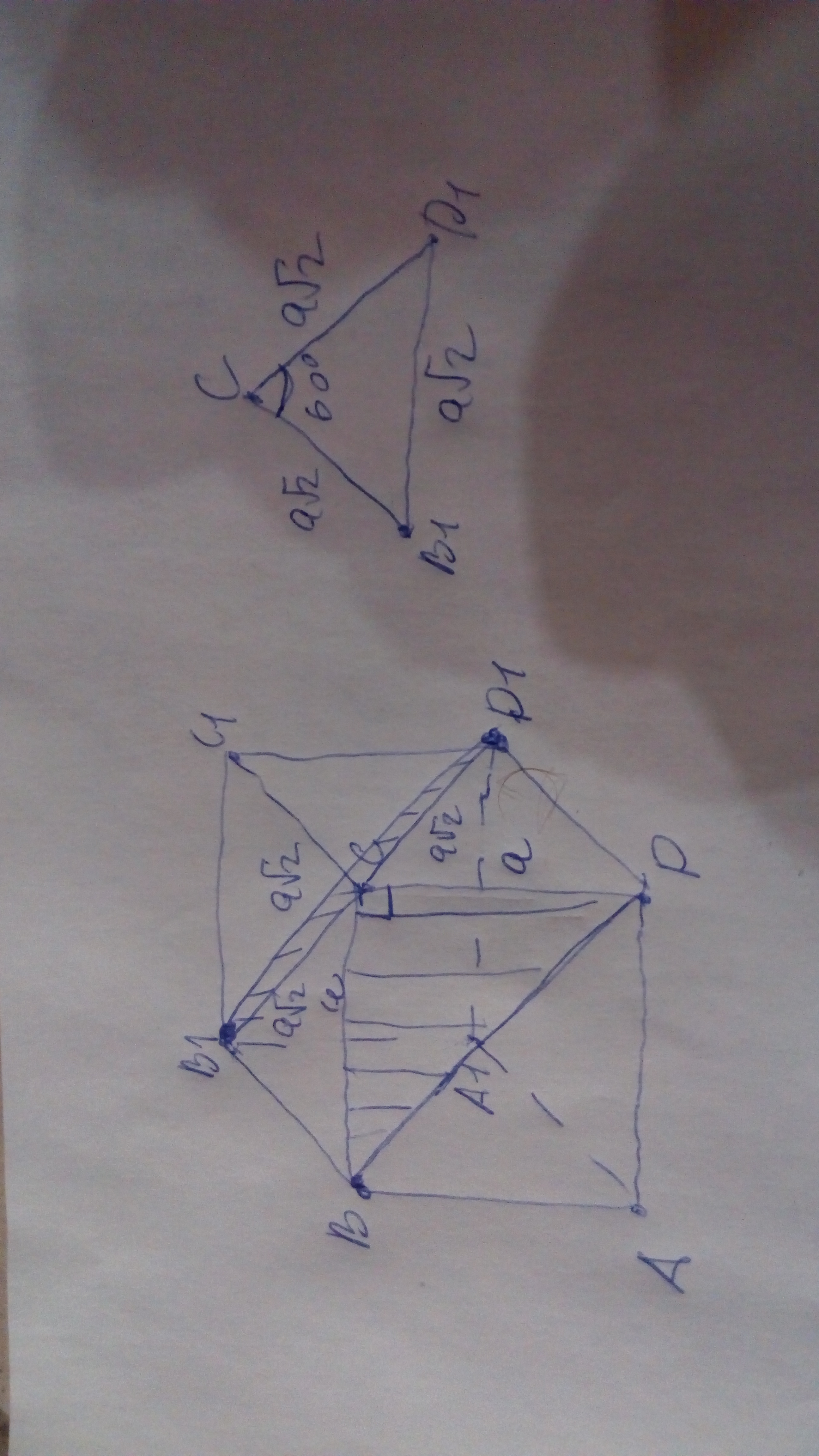
Плоскость ABC=ABCD. Проекция CB1D1 на ABCD,не что иное как треугольник CBD . Тогда если b-угол между плоскостями ABC и CB1D1,то cos(b)=S(CBD)/S(CB1D1) S-площадь. Пусть сторона куба равна a,тогда величина диагонали равна :a*√2 (Из теоремы Пифагора). Очевидно,что треугольник :CB1D1-равносторонний,со стороной a*√2. А треугольник CBD-прямоугольно-равнобедренный ,с величиной катета a. S(CB1D1)=( (a*√2)^2 *√3) )/4 = = ( a^2*√3)/2 S(CBD)=a^2/2. Откуда : cos(b)=(a^2/2)/ ( (a^2*√3)/2)= =1/√3=√3/3. b=arccos(√3/3). P.S кто то очень умный,скажет что этот угол можно точно посчитать,а вот и нет,это можно было бы посчитать,только для тангенса.

Answer 2

Можно конечно искать 3 стороны,теорема косинусов,но так неудобно.