Question

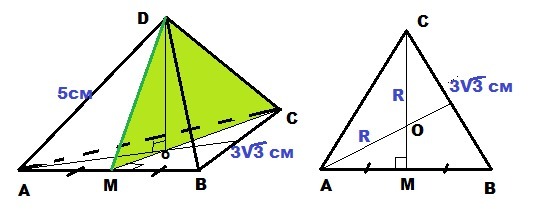
ДАВС-правильная треугольная пирамида,сторона основания 3 корня из 3 см,а боковое ребро 5 см. МС-медиана треугольника АВС. Найти площадь треугольника МДС?

Answer 1

Дано: сторона основания а = 3√3 см и боковое ребро L = 5 см.

Отрезок ДМ - это апофема боковой грани.
ДМ = √L² - (a/2)²) = √(25 - (27/4)) = √(73/4) = √73/2 ≈  4,2720019 см.
Медиана МС = а√3/2 = 3√3*√3/2 = 9/2 = 4,5 см.
Площадь треугольника МДС находим по формуле Герона:
a = 5, b = 4,5, c = √73/2 = 4,2720019. 
ДС = √(p(p-a)(p-b)(p-c)) =  9 см².
Здесь р =   6,886001.

Answer 2

Основание пирамиды - равносторонний треугольник ΔABC
AB = BC = AC = 3√3 см
Медиана CM также высота и биссектриса ⇒
CM = CB * sin 60° = 3√3 * √3/2 = 9/2 = 4,5 см

Пирамида DABC - правильная  ⇒   высота пирамиды DO опускается в центр вписанной/описанной окружности равностороннего треугольника основания. 
R = AO = AC / √3 = 3√3 / √3 = 3 см

ΔADO : ∠AOD = 90°;  AO = 3 см;  AD = 5 см
Теорема Пифагора
DO² = AD² - AO² = 5² - 3² = 16
DO = √16 = 4 см

$S_{MDC}= frac{1}{2} CM * DO = frac{1}{2} * 4,5 * 4 = 9$ см²

Ответ:  $S_{MDC}= 9$ см²