Предмет: Алгебра,
автор: STIKS333
Исследовать график
1) Область определения, непрерывность, четность/нечётность, периодичность функции.
2) Асимптоты графика функции.
3) Нули функции, интервалы знакопостоянства.
4) Возрастание, убывание и экстремумы функции.
5) Выпуклость, вогнутость и перегибы графика.
6) Дополнительные точки и график по результатам исследования.
Приложения:
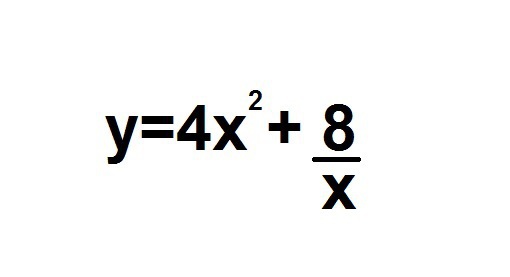
Ответы
Автор ответа:
0
y=4x²+8/x
D(y)⇒(-∞;0) U (0;∞)
Функция не существует при х=0,следовательно х=0 вертикальная асиптота
y(-x)=4(-x)²+8/(-x)=4x²-8/x ни четная,ни нечетная
y=0 4x²+8/x=(4x³+8)/x=0⇒4x³=-8⇒x=-∛2
(-∛2;0) точка пересечения с осями
y`=8x-8/x²=(8x³-8)/x²=0
8x³=8
x³=1
x=1
_ +
-------------------(1)--------------------
убыв min возр
y(1)=4*1+8/1=4+8=12
y``=8+16/x³=(8x³+16)/x³=0
8x³=-16
x³=-2
x=-∛2
_ +
-----------------------(-∛2)----------------------
выпукл вверх вогн вниз
y(-∛2)=0
(-∛2;0)точка перегиба
Дополнительные точки
(-2;12):(-1;-4);(1/2;17);(2;20)
D(y)⇒(-∞;0) U (0;∞)
Функция не существует при х=0,следовательно х=0 вертикальная асиптота
y(-x)=4(-x)²+8/(-x)=4x²-8/x ни четная,ни нечетная
y=0 4x²+8/x=(4x³+8)/x=0⇒4x³=-8⇒x=-∛2
(-∛2;0) точка пересечения с осями
y`=8x-8/x²=(8x³-8)/x²=0
8x³=8
x³=1
x=1
_ +
-------------------(1)--------------------
убыв min возр
y(1)=4*1+8/1=4+8=12
y``=8+16/x³=(8x³+16)/x³=0
8x³=-16
x³=-2
x=-∛2
_ +
-----------------------(-∛2)----------------------
выпукл вверх вогн вниз
y(-∛2)=0
(-∛2;0)точка перегиба
Дополнительные точки
(-2;12):(-1;-4);(1/2;17);(2;20)
Приложения:
Автор ответа:
0
Разве нет у функции наклонной а симптомы?
Похожие вопросы
Предмет: Математика,
автор: gebekova08
Предмет: История,
автор: olgamart1210
Предмет: Английский язык,
автор: Ivashibanov
Предмет: Биология,
автор: zebelovih
Предмет: Химия,
автор: AntonKo66