Предмет: Математика,
автор: volchenok1993
напишите уравнение касательной к графику функции f(x)=cos^2 6x в точке X0=pi/24
Приложения:
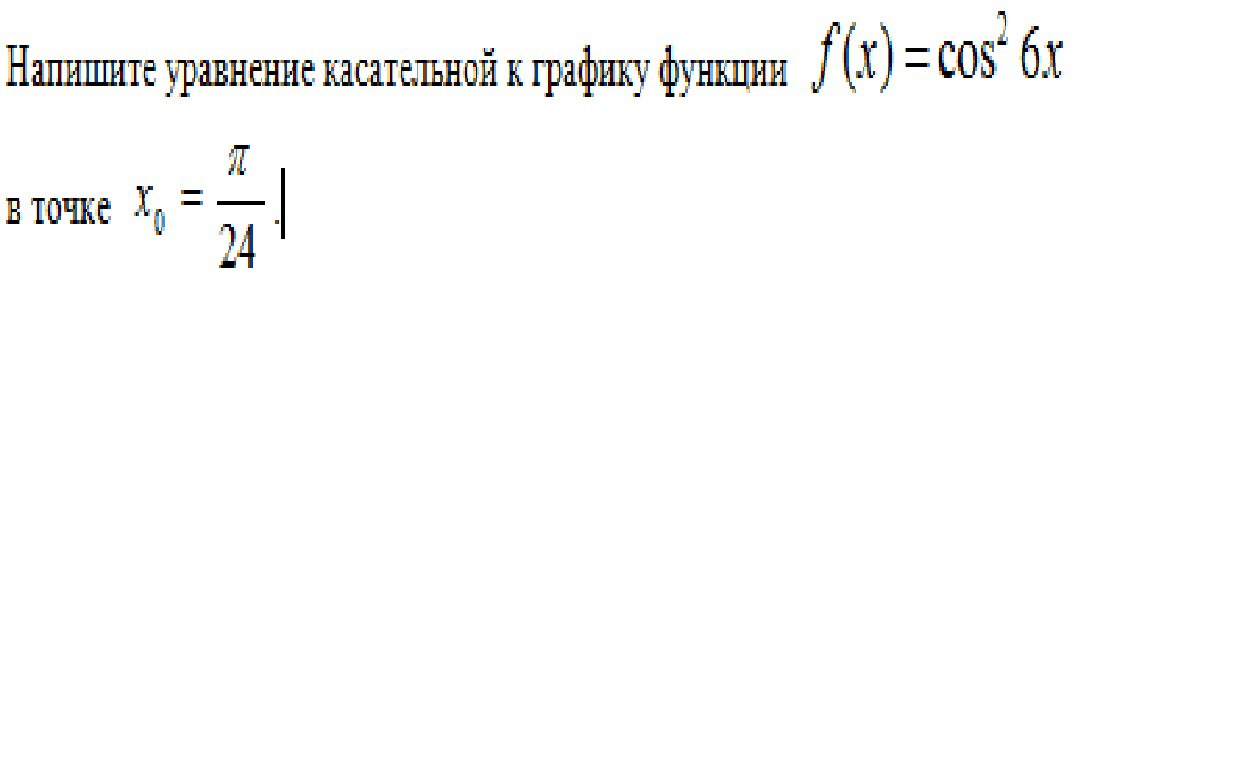
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Литература,
автор: grrd14
Предмет: География,
автор: andrejkabaluk9
Предмет: Химия,
автор: soffa17
Предмет: Алгебра,
автор: katyusha11
Предмет: Литература,
автор: zlodemira1