Question

К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно. Известно, что AB = 33, а периметр треугольника ABC равен 103. НАйти периметр треугольника CPQ.
Нашел чему равно PQ. PQ=18.5 

Answer 1

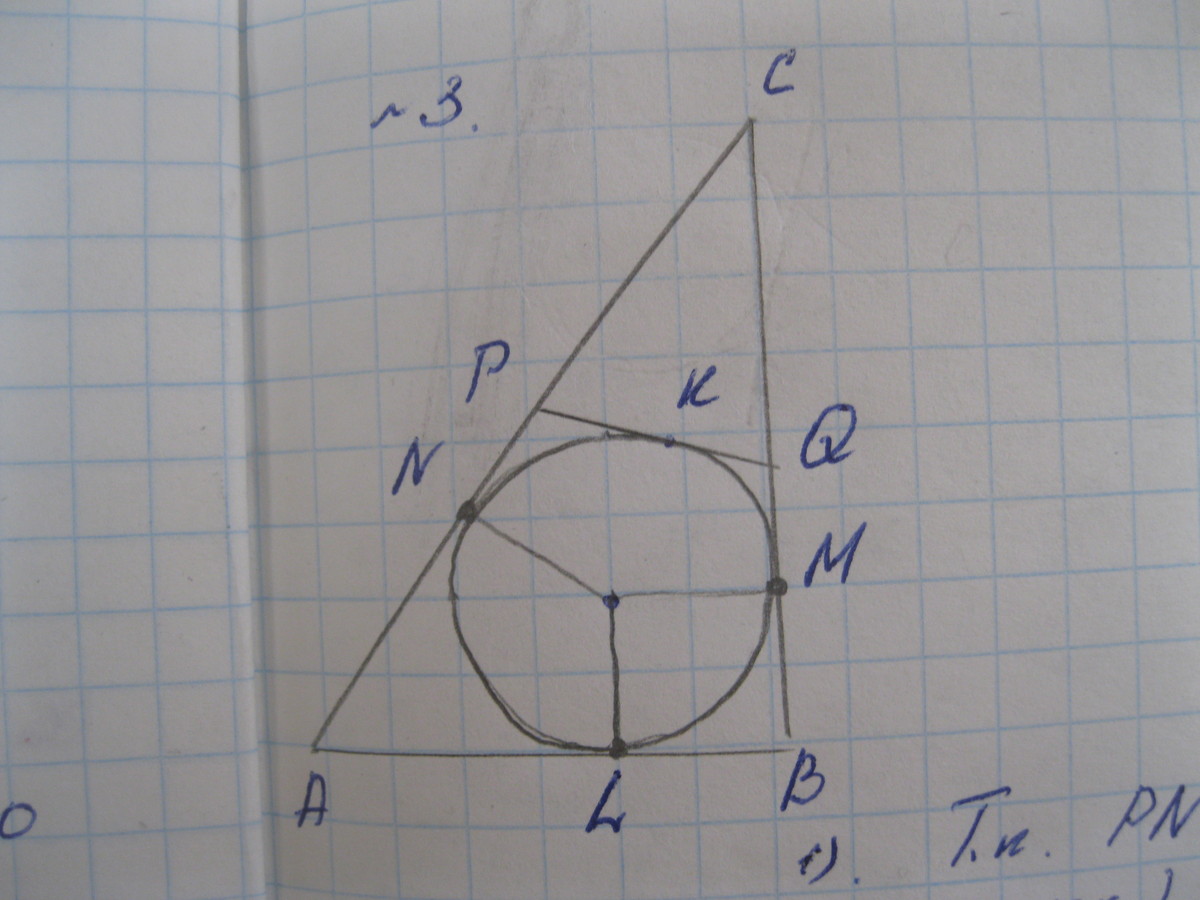
1. Т.к. PN=PK и KQ=QM (по свойству касательных), то СN+CM=P треуг. CPQ
2. Т.к. AN=AL и MB=BL, то AN+NB=AB (по св-ву касательных)
3. P треуг. ABC= AB+BC+AC, где BC=CM+MB; AC=CN+AN
Получим: AB+CM+MB+CN+AN=103  (выделенные величины равно, поэтому их складываем)
AB+2CM+MB+AN=103 (см. пункт 2.)
2AB+2CM=103
2(AB+CM)=103
AB+CM=51,5
Отсюда CM=51,5-33=18,5
4. Т.к. CN+CM=P треуг. СPQ и CN=CM (по св-ву касат.), то P треуг. CPQ=2CM=2*18,5=37