Предмет: Геометрия,
автор: sponser
Знайдіть висоту правильної чотирикутної піраміди, всі ребра якої дорівнюють
Ответы
Автор ответа:
0
диагональ основания равна 2sqrt(2)*sqrt(2)=4
половина диаrорали = 2
высота (по т.Пифагора)
Автор ответа:
0
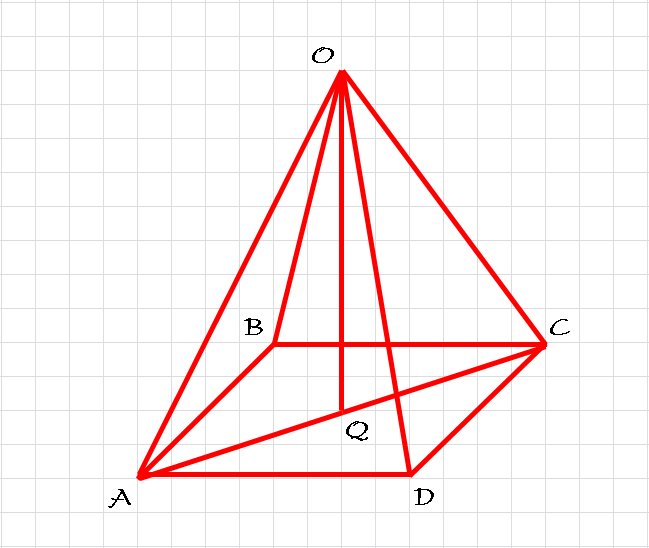
Из треугольника ADC (угол D прямой) по теореме Пифагора находим:
Из треугольника AQO (угол Q прямой) по теореме Пифагора находим:
Ответ: 2
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: akathrine90Катрин
Предмет: Қазақ тiлi,
автор: safiaskan
Предмет: Математика,
автор: Аноним
Предмет: Обществознание,
автор: Linale