Предмет: Математика,
автор: Animashka228
Постройте график функции
Приложения:

Ответы
Автор ответа:
0
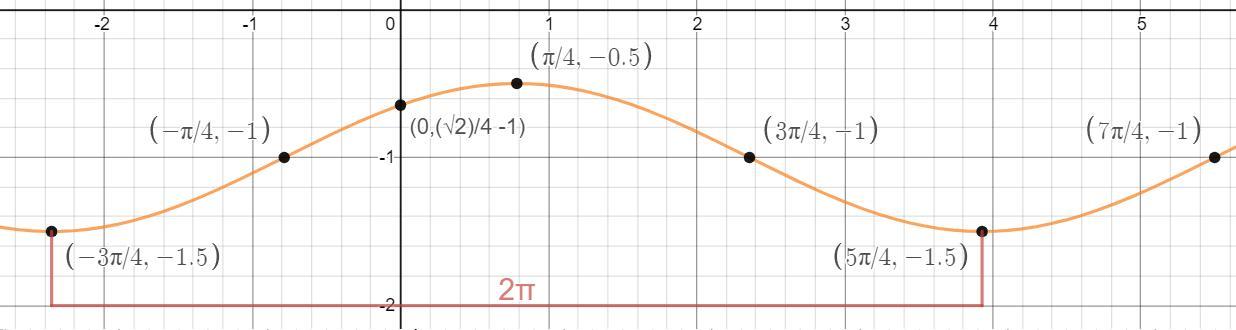
Функция будет выглядеть как sin x, только её ординаты будут уменьшены в 2 раза, затем опущены на 1, а сама функция будет сдвинута влево на π/4. Это я к тому, что функция периодическая.
Можно построить как я расписал (последовательно), а можно сразу, так просто меньше считать надо, но если вам просто нужно примерный вид графика функции, то обычно строят последовательно.
Найдём точки пересечения с осями координат:
Найдём абсциссы экстремумов функции:
Найдём ординаты экстремумов:
Найдём абсциссы точек перегиба:
Ордината точки перегиба будет (-1.5+(-0.5))/2= -1.
Как будет выпукла функция можно определить по тому, что это sin x. Сам график смотри внизу.
Кстати период функции 2π.
Приложения:
Похожие вопросы
Предмет: География,
автор: Alexandr12345678910
Предмет: Українська мова,
автор: razrusitelfercuk
Предмет: История,
автор: laskivnickasofia
Предмет: Химия,
автор: tunechiluv1
Предмет: Математика,
автор: kamillaorl