Предмет: Алгебра,
автор: Brain087
Помогите, пожалуйста решить 199 номер (2). Необходимо решение. Заранее спасибо.
Приложения:
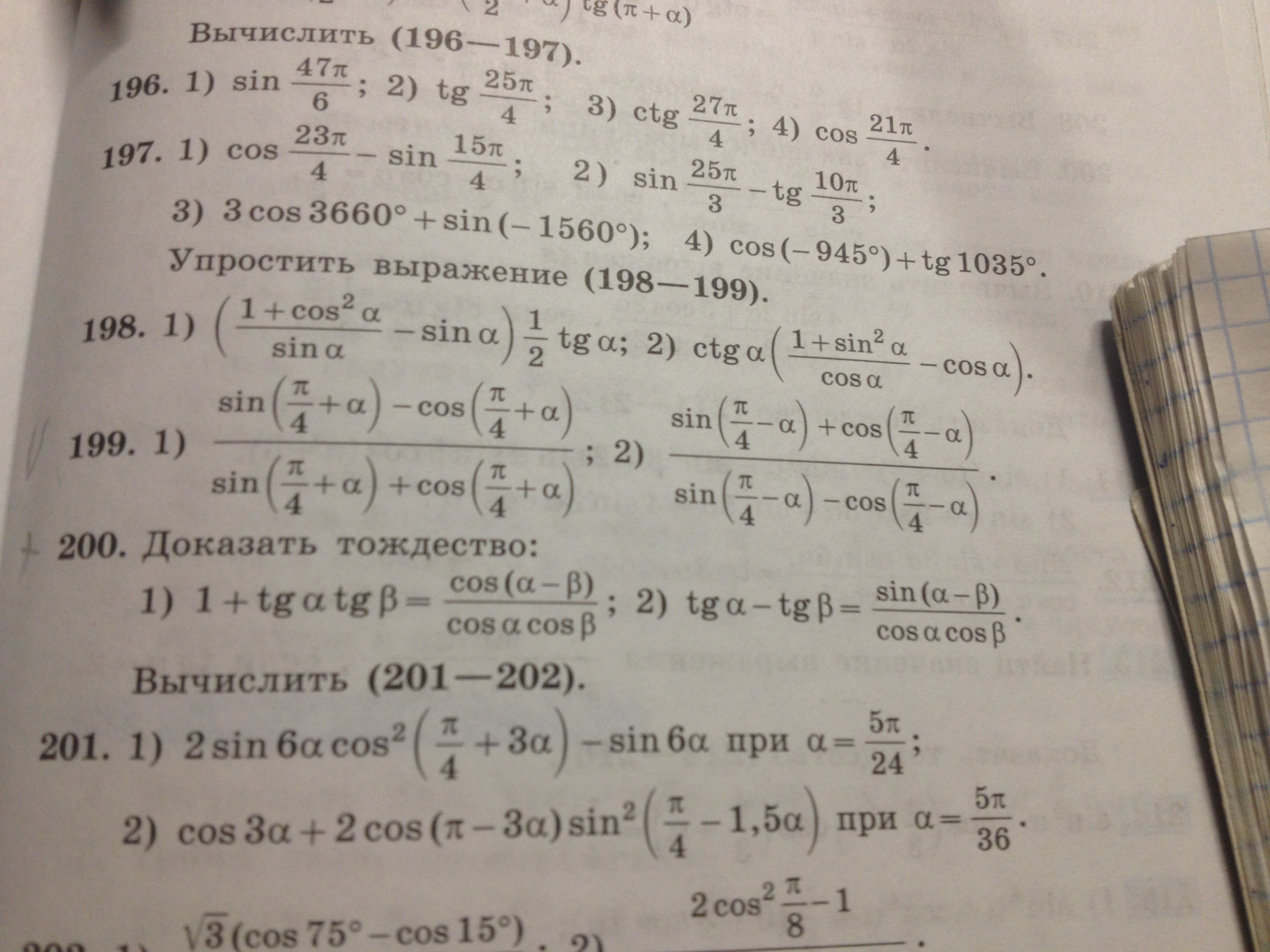
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Информатика,
автор: merk8700
Предмет: Математика,
автор: matveyfoykin74
Предмет: Алгебра,
автор: Ritulik92
Предмет: Литература,
автор: Chagin24
Предмет: Математика,
автор: salatanat82