Предмет: Алгебра,
автор: Theme168PO
построить график функции y=2cos2x
Ответы
Автор ответа:
0
у cosx период 2pi, значит у cos(2x) период будет 2pi/2=pi
рассмотрим функцию на промежутке периода
возьмем промежуток![[ -frac{pi}{2} ; frac{pi}{2} ] [ -frac{pi}{2} ; frac{pi}{2} ]](https://tex.z-dn.net/?f=+%5B+-frac%7Bpi%7D%7B2%7D+%3B+frac%7Bpi%7D%7B2%7D+%5D)
ищем нули:
![y=0
\2cos(2x)=0
\cos(2x)=0
\2x= frac{pi}{2} +pi n
\x= frac{pi}{4} + frac{pi n}{2}
\n=0; x=frac{pi}{4} in [ -frac{pi}{2} ; frac{pi}{2} ]
\n=1; x=frac{3pi}{4} notin [ -frac{pi}{2} ; frac{pi}{2} ]
\n=-2; x=-frac{pi}{4} in [ -frac{pi}{2} ; frac{pi}{2} ]
\x=0
\y=2*cos(0)=2*1=2 y=0
\2cos(2x)=0
\cos(2x)=0
\2x= frac{pi}{2} +pi n
\x= frac{pi}{4} + frac{pi n}{2}
\n=0; x=frac{pi}{4} in [ -frac{pi}{2} ; frac{pi}{2} ]
\n=1; x=frac{3pi}{4} notin [ -frac{pi}{2} ; frac{pi}{2} ]
\n=-2; x=-frac{pi}{4} in [ -frac{pi}{2} ; frac{pi}{2} ]
\x=0
\y=2*cos(0)=2*1=2](https://tex.z-dn.net/?f=y%3D0%0A%5C2cos%282x%29%3D0%0A%5Ccos%282x%29%3D0%0A%5C2x%3D+frac%7Bpi%7D%7B2%7D+%2Bpi+n%0A%5Cx%3D+frac%7Bpi%7D%7B4%7D+%2B+frac%7Bpi+n%7D%7B2%7D+%0A%5Cn%3D0%3B+x%3Dfrac%7Bpi%7D%7B4%7D+in+%5B+-frac%7Bpi%7D%7B2%7D+%3B+frac%7Bpi%7D%7B2%7D+%5D%0A%5Cn%3D1%3B+x%3Dfrac%7B3pi%7D%7B4%7D+notin+%5B+-frac%7Bpi%7D%7B2%7D+%3B+frac%7Bpi%7D%7B2%7D+%5D%0A%5Cn%3D-2%3B+x%3D-frac%7Bpi%7D%7B4%7D+in+%5B+-frac%7Bpi%7D%7B2%7D+%3B+frac%7Bpi%7D%7B2%7D+%5D%0A%5Cx%3D0%0A%5Cy%3D2%2Acos%280%29%3D2%2A1%3D2)
теперь ищем точки границы интервала:
cos - четная функция, значит:

получили точки:

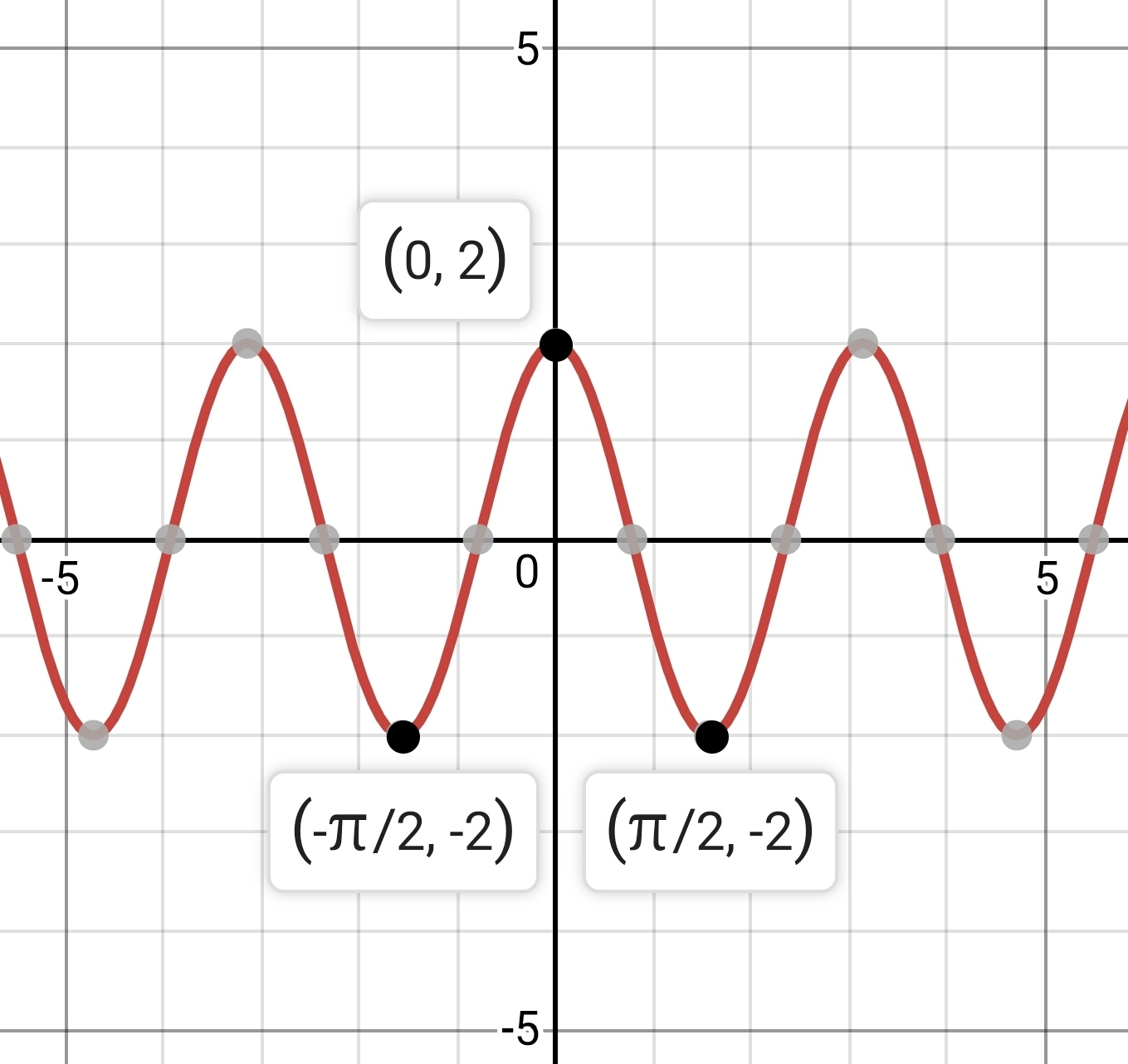
строим график:
берем график cosx, сжимаем вдоль оси x в 2 раза получаем график cos(2x), затем растягиваем его вдоль оси y в 2 раза, получим график функции 2cos(2x)
и также он будет проходит через вышеуказанные точки.
График в приложении.
рассмотрим функцию на промежутке периода
возьмем промежуток
ищем нули:
теперь ищем точки границы интервала:
cos - четная функция, значит:
получили точки:
строим график:
берем график cosx, сжимаем вдоль оси x в 2 раза получаем график cos(2x), затем растягиваем его вдоль оси y в 2 раза, получим график функции 2cos(2x)
и также он будет проходит через вышеуказанные точки.
График в приложении.
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: astyash
Предмет: Химия,
автор: ukopiam
Предмет: Физика,
автор: daraserbina65
Предмет: Алгебра,
автор: Полинка2311
Предмет: Литература,
автор: 1111111111111ааа