Question

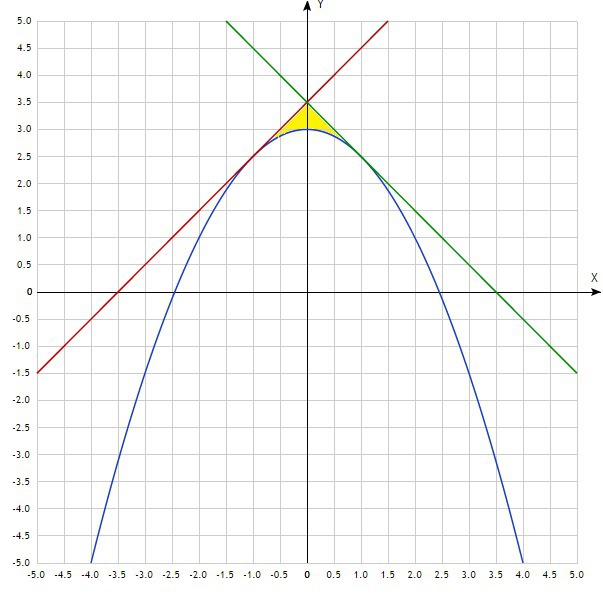
Вычислите площадь фигуры, ограниченной графиком функции у=-0.5х^2+3 и двумя касательными к этому графику, проходящими через точки на оси оу и образующими между собой прямой угол.

Answer 1

Найдём касательные к графику функции y=-0,5x²+3. График указанной функции представляет собой параболу ветви которой направлены вниз, вершина находится в точке с координатами (0;3), ось симметрии совпадает с осью ординат. Касательные (из условия) перпендикулярны друг другу и равны, следовательно угол наклона к оси абсцисс одной из них будет 45°, а другой 135°. Угловой коэффициент k прямой равен тангенсу угла наклона, значит у одной касательной он будет
k₁=tg45°=1
а у другой 
k₂=tg135°=-1
Тогда уравнения касательных примут вид
y₁=x+b
y₂=-x+b
Найдём значение b, для этого приравняем функции y=-0,5x²+3 и y=x+b:
-0,5x²+3=x+b
-0,5x²+3-x-b=0
-0,5x²-x+(3-b)=0
Уравнение должно иметь один корень, значит дискриминант должен быть равен 0
D=(-1)²-4*(-0,5)*(3-b)=1+2(3-b)=1+6-2b=7-2b=0
-2b=-7
b=3,5
Уравнения касательных будут иметь вид:
y=x+3,5
y=-x+3,5
Находим пределы интегрирования. Сначала нижний:
-0,5x²+3=x+3,5
-0,5x²-x-0,5=0
D=0
x=1/(-0,5*2)=-1
Теперь верхний:
-0,5x²+3=-x+3,5
-0,5x²+x-0,5
D=0
x=-1/(-0,5*2)=1
Найдём площадь фигуры сначала слева от оси ординат, потом справа и сложим их:
$S= intlimits^0_{-1} {((x+ frac{7}{2})-(- frac{1}{2}x^2+3))} , dx +intlimits^1_0 {((-x+ frac{7}{2})-(- frac{1}{2}x^2+3)) } , dx$
$=intlimits^0_{-1} {(frac{1}{2}x^2+x+ frac{1}{2})} , dx +intlimits^1_0 {( frac{1}{2}x^2-x+ frac{1}{2}) } , dx=$
$= (frac{x^3}{6}+ frac{x^2}{2}+ frac{x}{2}|_{-1}^0)+(frac{x^3}{6}- frac{x^2}{2}+ frac{x}{2}|_0^1)=0-( -frac{1}{6}+ frac{1}{2} - frac{1}{2})+ frac{1}{6} - frac{1}{2}+ frac{1}{2}$
$=frac{1}{6}- frac{1}{2} + frac{1}{2}+ frac{1}{6} - frac{1}{2}+ frac{1}{2} = frac{2}{6}= frac{1}{3}$ ед².