Предмет: Алгебра,
автор: trashkov99
Найдите наименьшее значение выражения (6x+5y-3)^2 + (2x+3y+3)^2 и значения x и y, при которых оно достигается. Я уже 3й час сижу... Не могу решить, помогите пожалуйста.
Ответы
Автор ответа:
0
Сумма двух неотрицательных величин(в данном случае — это  и
и  ) не может быть отрицательной, т.е. всегда выполняется
) не может быть отрицательной, т.е. всегда выполняется  и
и  . Соответственно, наименьшим значением выражения
. Соответственно, наименьшим значением выражения  будет ноль. Поэтому решаем уравнение
будет ноль. Поэтому решаем уравнение  .
.

Сумма двух неотрицательных величин равна нулю тогда и только тогда, когда каждая из них равна нулю. Отсюда система уравнений:
см. приложение.
Ответ: .
.
Сумма двух неотрицательных величин равна нулю тогда и только тогда, когда каждая из них равна нулю. Отсюда система уравнений:
см. приложение.
Ответ:
Приложения:
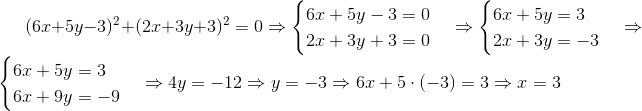
Похожие вопросы
Предмет: Українська мова,
автор: degtarola3
Предмет: Українська мова,
автор: violetta14015014
Предмет: Биология,
автор: Ezenhaim
Предмет: Математика,
автор: лесераса
Предмет: Алгебра,
автор: weasf