Question

вычислите площадь плоской фигуры,ограниченной прямой y=0,параболой y=2x-x^2 и касательной,проведенной к этой параболе в точке (0.5;0,75)

Answer 1

Найдём касательную к параболе в точке (0,5;0,75). Уравнение касательной имеет вид:
y=f'(x₀)(x-x₀)+f(x₀)
x₀=0,5
f(x₀)=0,75
f'(x)=(2x-x²)'=2-2x
f'(x₀)=2-2*0,5=2-1=1
Подставляем все найденные значения в уравнение касательной:
y=1*(x-0,5)+0,75=x-0,5+0,75=x+0,25
Площадь фигуры, ограниченной графиками функций находится по формуле:
S=∫(f(x)-g(x))dx
Верхний предел интегрирования будет равен 0,5 или 1/2 (точка касания прямой и параболы), а нижний предел интегрирования равен
x+0,25=0
x=-0,25=-1/4 (точка пересечения касательной с прямой y=0 или осью абсцисс)
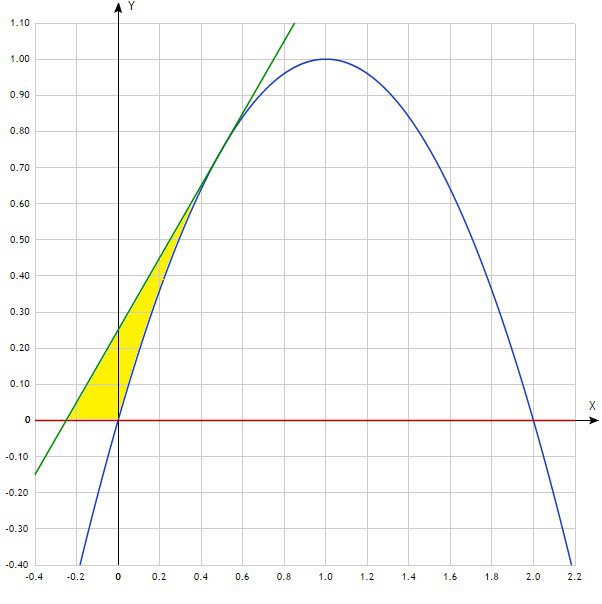
Предлагаю начертить графики на координатной плоскости. Где сразу видны пределы интегрирования и график функции y=x+0,25 расположен выше графика функции y=2x-x². Записываем интеграл и решаем его:
$S= intlimits^{ frac{1}{2} }_{- frac{1}{4} } {((x+0,25)-(2x-x^2))} , dx =intlimits^{ frac{1}{2} }_{- frac{1}{4} } {(x+0,25-2x+x^2)} , dx=$
$=intlimits^{ frac{1}{2} }_{- frac{1}{4} } {(x^2-x+ frac{1}{4} )} , dx= frac{x^3}{3} - frac{x^2}{2} + frac{x}{4} |_{- frac{1}{4} }^{ frac{1}{2} }= frac{1}{24}- frac{1}{8} + frac{1}{8}+ frac{1}{192} + frac{1}{32}+ frac{1}{16}$
$= frac{8+1+6+12}{192} = frac{27}{192}= frac{9}{64}$ ед²