Предмет: Алгебра,
автор: poukot668
Решите пожалуйста, очень надо
Приложения:
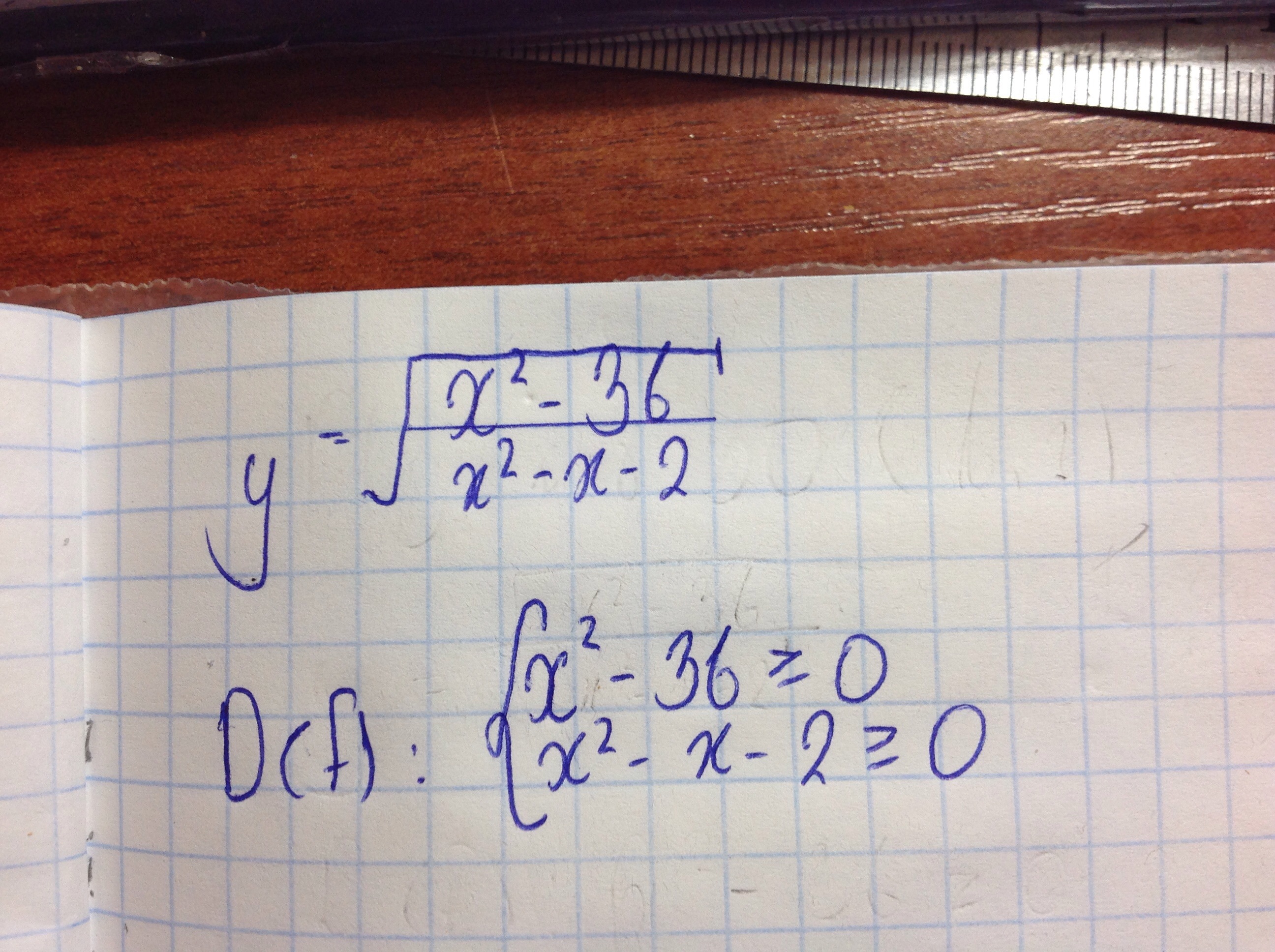
Ответы
Автор ответа:
0
В задании, очевидно, надо определить область определения функции
(так и надо было в задании написать!!!).


Находим решение этих неравенств:
х² - 36 ≥ 0, х² ≥ 36, х₁ ≥ 6, х₂ ≤ -6.
Исходим их того, что числитель и знаменатель дроби положительны, так как в числителе х² - 36 переменная х² не может быть отрицательным числом.
х² - х - 2 ≥ 0.
Разложим трёхчлен на множители, приравняв его нулю.
х² - х - 2 = 0
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-1)^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√9-(-1))/(2*1)=(3-(-1))/2=(3+1)/2=4/2=2;x₂=(-√9-(-1))/(2*1)=(-3-(-1))/2=(-3+1)/2=-2/2=-1.
Теперь можно преобразовать исходное неравенство:
(х - 2)(х + 1) ≥ 0.
Здесь возможны 2 варианта - или оба множители положительны, или оба отрицательны:
х - 2 ≥ 0, х₃ ≥ 2,
х + 1 ≥ 0, х₄ ≥ -1.
х - 2 ≤ 0, х₅ ≤ 2,
х + 1 ≤ 0, х₆ ≤ -1.
Общим является решение: х≥ 6, х ≤ -6.
(так и надо было в задании написать!!!).
Находим решение этих неравенств:
х² - 36 ≥ 0, х² ≥ 36, х₁ ≥ 6, х₂ ≤ -6.
Исходим их того, что числитель и знаменатель дроби положительны, так как в числителе х² - 36 переменная х² не может быть отрицательным числом.
х² - х - 2 ≥ 0.
Разложим трёхчлен на множители, приравняв его нулю.
х² - х - 2 = 0
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-1)^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√9-(-1))/(2*1)=(3-(-1))/2=(3+1)/2=4/2=2;x₂=(-√9-(-1))/(2*1)=(-3-(-1))/2=(-3+1)/2=-2/2=-1.
Теперь можно преобразовать исходное неравенство:
(х - 2)(х + 1) ≥ 0.
Здесь возможны 2 варианта - или оба множители положительны, или оба отрицательны:
х - 2 ≥ 0, х₃ ≥ 2,
х + 1 ≥ 0, х₄ ≥ -1.
х - 2 ≤ 0, х₅ ≤ 2,
х + 1 ≤ 0, х₆ ≤ -1.
Общим является решение: х≥ 6, х ≤ -6.
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: andrey67008
Предмет: Геометрия,
автор: kostasperfilie
Предмет: Математика,
автор: RomaMoxitov