Предмет: Математика,
автор: gelyatsareva9
найти интеграл
∫x³*√x^4+1 dx
Приложения:
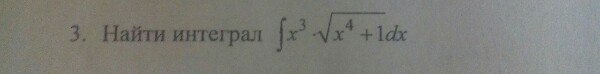
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: matvejhorov796
Предмет: Геометрия,
автор: si1805475
Предмет: ОБЖ,
автор: zannakalinicenko67
Предмет: Обществознание,
автор: Ekaterina1819
Предмет: Алгебра,
автор: CATSWAG