Предмет: Алгебра,
автор: kikvoronune
Помогите , пожалуйста, решить данный интеграл , а то у меня бред выходит какой-то. Прошу не решать по решению интегралов онлайн
Приложения:
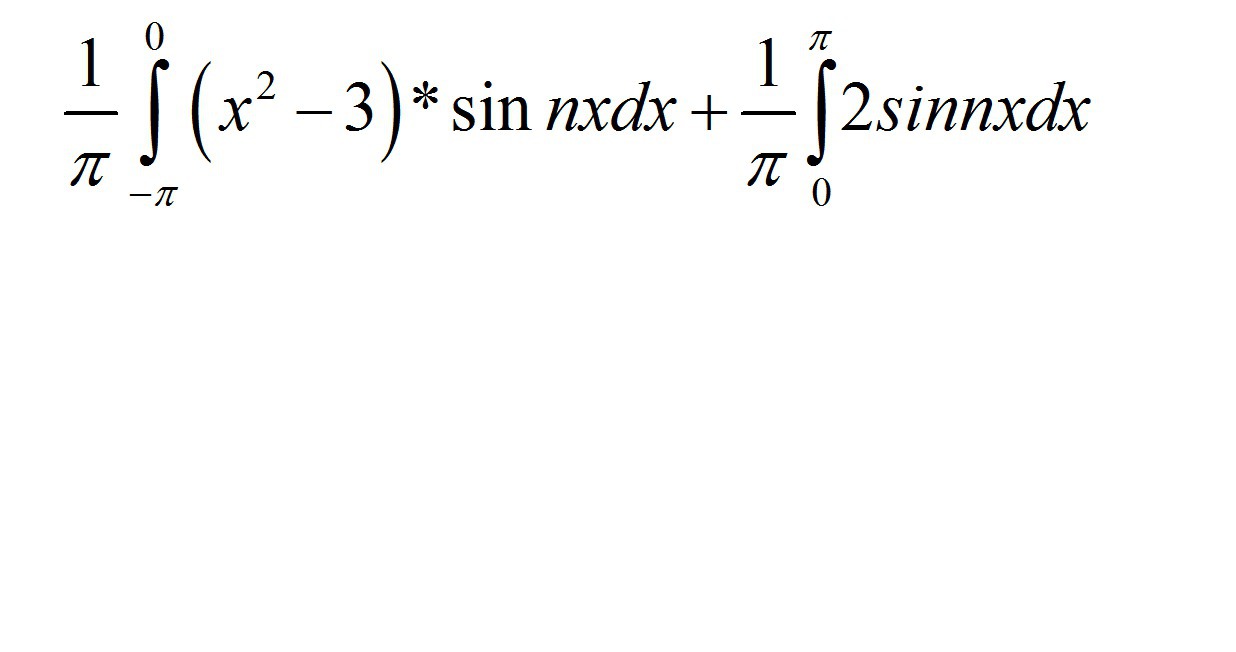
Ответы
Автор ответа:
0
Автор ответа:
0
и все же, тут тоже ужас выходит. И это теперь надо подставить в сумму разложения фурье :D
Автор ответа:
0
Ну там была система (x^2-3) от -pi до 0, и просто 2 , промежуток от 0 до pi, так что думаю так для коэффициента Bn
Автор ответа:
0
Тогда верно. Когда функция задана системой,то такое бывает.
Похожие вопросы
Предмет: Алгебра,
автор: HOCHUOTVETI
Предмет: Математика,
автор: veronikabondarenko20
Предмет: Математика,
автор: saltanatbulekbaeva27
Предмет: История,
автор: kudyakov
Предмет: Математика,
автор: землеройка