Предмет: Алгебра,
автор: prostokvasha
тригонометрические уравнения с одз
срочно нужно решить,заранее спасибо
Приложения:
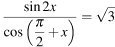

Ответы
Автор ответа:
0
1) sin2x/ cos(π/2 + x) = √3;
cos(π/2 + x) = - sinx ≠ 0;
x ≠ π*k; k∈Z.
sin 2x = 2 sin x cos x;⇒
2 sin x * cos x / - sin x = √ 3;
- 2 cos x = √ 3;
cos x = - √ 3/2;
x = + - 5 π/6 + 2πk; k -Z
1) 2 cos x + 1 / tg x - √ 3 = 0;
tg x - √ 3 ≠ 0;
tg x ≠ √ 3;
x ≠ π/3 + πk; k-Z.
2 cos x + 1 = 0;
cos x = - 1/2;
x = 2π/3 + 2πk; k-Z ∈ одз;
x = - 2π/3 + 2πk; k-Z ∉ одз.
Ответ х = 2π/3 + 2πk; k-Z
cos(π/2 + x) = - sinx ≠ 0;
x ≠ π*k; k∈Z.
sin 2x = 2 sin x cos x;⇒
2 sin x * cos x / - sin x = √ 3;
- 2 cos x = √ 3;
cos x = - √ 3/2;
x = + - 5 π/6 + 2πk; k -Z
1) 2 cos x + 1 / tg x - √ 3 = 0;
tg x - √ 3 ≠ 0;
tg x ≠ √ 3;
x ≠ π/3 + πk; k-Z.
2 cos x + 1 = 0;
cos x = - 1/2;
x = 2π/3 + 2πk; k-Z ∈ одз;
x = - 2π/3 + 2πk; k-Z ∉ одз.
Ответ х = 2π/3 + 2πk; k-Z
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Биология,
автор: Аноним
Предмет: Биология,
автор: makmary1
Предмет: Математика,
автор: добрая12
Предмет: Литература,
автор: altingul130