Предмет: Алгебра,
автор: Elechka777
Найти интегралы: (полное решение) задания на изображении
Приложения:
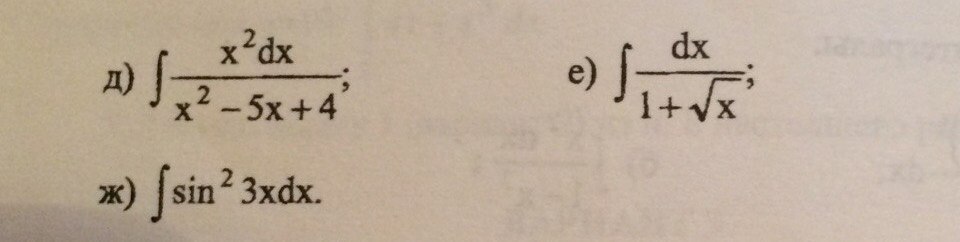
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Обществознание,
автор: alexwasp2p39nk3
Предмет: Физика,
автор: angelinamanzaj
Предмет: География,
автор: dasenkadasenka6
Предмет: Химия,
автор: sfo
Предмет: Математика,
автор: oksidi