Предмет: Алгебра,
автор: Elechka777
Помогите с решением интегралов
Приложения:
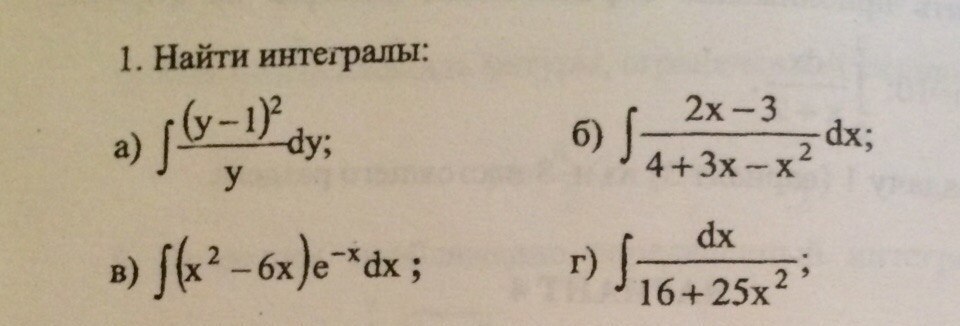
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: lilia198518
Предмет: Английский язык,
автор: sviridova448
Предмет: Математика,
автор: МиланаАнтиповаТВ