Предмет: Математика,
автор: АннаК96
Ребят, помогите пожалуйста с математикой. Исследование функции, очень прошу.
Исследовать функцию методом дифференциального исчисления и построить график. у=((х-1)^2)/(х^2). План такой: 1. Область определения функции, четная или нет. 2. Точки разрыва, есть или нет, если есть, то какого рода. 3.Нули функции и промежутки знаков постоянных(><)? т.е начертить ось и на ней показать. 4. Монотонность и экстремумы (критические точки), + нарисовать ось и на ней показать максимум, минимум и точки разрыва, если есть. 5. Выпуклость и точки перегиба + ось и на ней показать где она выпуклая, а где нет. 6. Асимптоты (горизонтальная,вертикальная,наклонная). 7.График. Только нужно подробно, по-другому не засчитают Т__т, особенно про расчет производных.
Ответы
Автор ответа:
0
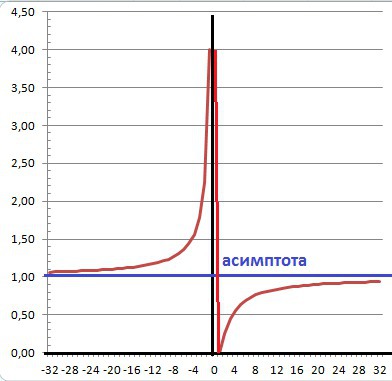
ДАНО

ИССЛЕДОВАНИЕ.
1. Область определения - х≠0 или
Х∈(-∞,0)∪(0,+∞)
2.Пересечение с осью Х. Y(x)= 0.
Х= 1.
3. Поведение в близи точки разрыва.
lim(0) = +∞.
4. Поведение на бесконечности
lim(-∞) = 1.
lim(+∞) = 1.
5. Асимптота Y=1.
6. Исследование на четность.

Функция ни четная ни нечетная.
7. Производная функции

Точка экстремума - Х=1.
Возрастает - Х∈(-∞,0)∪[1,+∞)
Убывает - X∈(0,1].
8 Минимальное значение
Ymin= 0.
Максимальное значение
Ymax = +∞
9. Графики прилагаются. Обратить на поведение в интервале от 0 до+1
ИССЛЕДОВАНИЕ.
1. Область определения - х≠0 или
Х∈(-∞,0)∪(0,+∞)
2.Пересечение с осью Х. Y(x)= 0.
Х= 1.
3. Поведение в близи точки разрыва.
lim(0) = +∞.
4. Поведение на бесконечности
lim(-∞) = 1.
lim(+∞) = 1.
5. Асимптота Y=1.
6. Исследование на четность.
Функция ни четная ни нечетная.
7. Производная функции
Точка экстремума - Х=1.
Возрастает - Х∈(-∞,0)∪[1,+∞)
Убывает - X∈(0,1].
8 Минимальное значение
Ymin= 0.
Максимальное значение
Ymax = +∞
9. Графики прилагаются. Обратить на поведение в интервале от 0 до+1
Приложения:

Похожие вопросы
Предмет: Математика,
автор: d36507066
Предмет: Қазақ тiлi,
автор: Romashka010
Предмет: История,
автор: oskarmolenda1
Предмет: Алгебра,
автор: 99Алёна
Предмет: Геометрия,
автор: Aлександpa