Предмет: Алгебра,
автор: Julia0fox
Решить неравенство (фото)
Приложения:
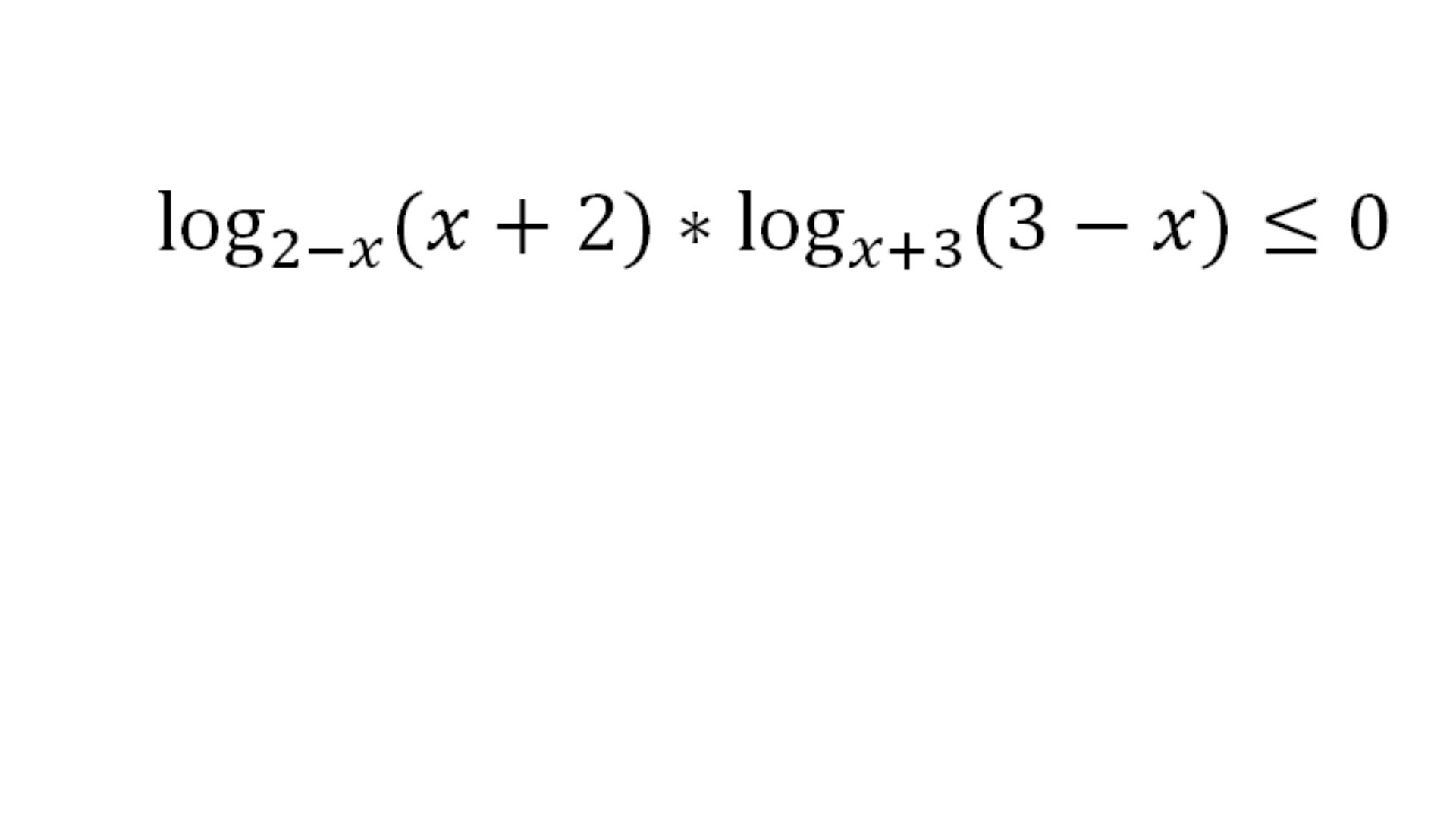
Ответы
Автор ответа:
0
решим отдельно неравенство(без учёта всех ограничений)
решений нету, по этому следующая совокупность:
эквивалентна системе:
решим отдельно неравенство(без учета всех ограничений)
Решим отдельно неравенство(без учета всех ограничений)
как видно неравенство не имеет решений даже без учета всех ограничений
значит система:
эквивалентна системе:
Похожие вопросы
Предмет: Биология,
автор: veklenkoaleksandra20
Предмет: Українська література,
автор: mishachabanecy
Предмет: Қазақ тiлi,
автор: bakhydysenova
Предмет: Биология,
автор: ekoponeva