Предмет: Алгебра,
автор: Julia0fox
Дана функция (на картинке)
1) Используя определение производной, найти f ' (x).
Приложения:
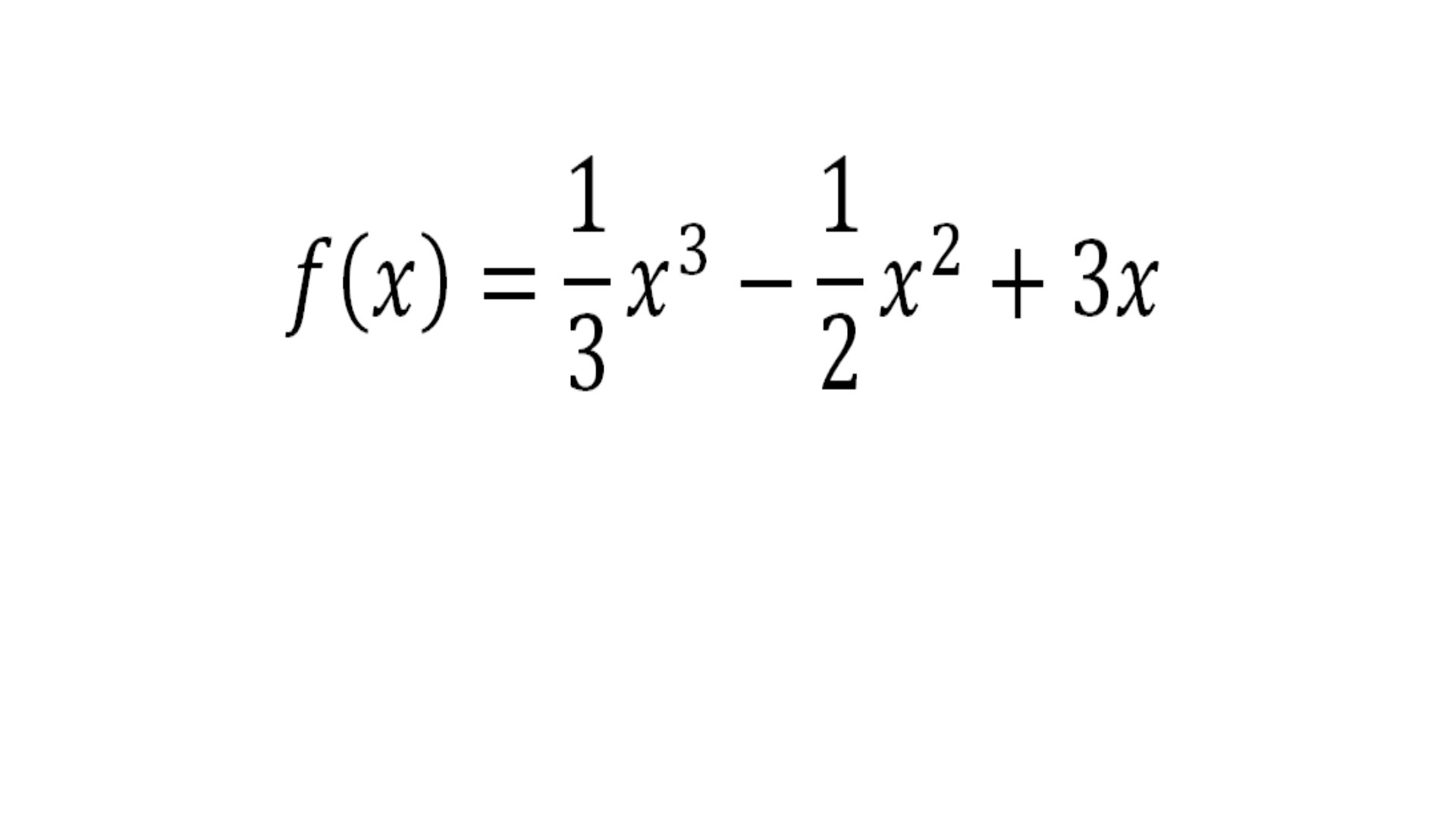
Ответы
Автор ответа:
0
f`(x)=3*1/3*x^2-2*1/2*x+3=x^2-x+3
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: VikaRine
Предмет: Английский язык,
автор: Vasa1233444
Предмет: Математика,
автор: aleksandra677
Предмет: Математика,
автор: otlichnicatani