Предмет: Алгебра,
автор: yana1241
ПОМОГИТЕ РЕШИТЬ ЧЕТЫРЕ ПРИМЕРА!!!СРОЧНО ПОЖАЛУЙСТА!!!
Приложения:
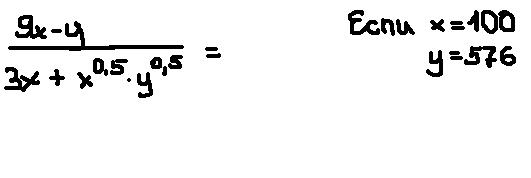
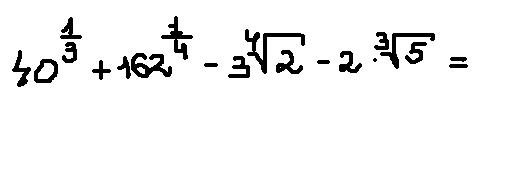
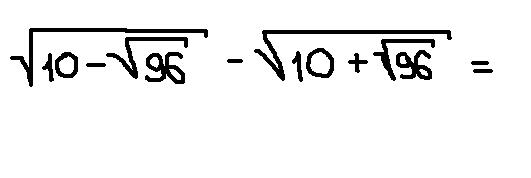
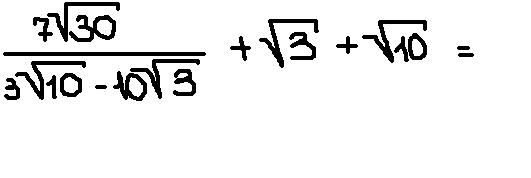
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: даня2272
Предмет: Русский язык,
автор: annakraeva13200
Предмет: Қазақ тiлi,
автор: Хохо1111
Предмет: Литература,
автор: msmadik63
Предмет: Геометрия,
автор: marya110386