Предмет: Алгебра,
автор: bogatovaekater
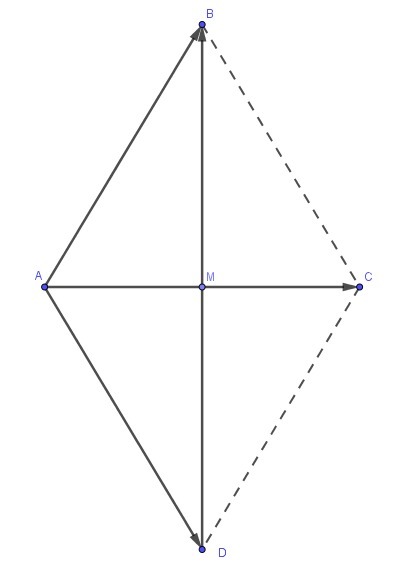
1.Диагонали ромба ABCD пересекаются в точке М.
1) Выразите вектор AM через векторы AB и BC
2) Найдите вектор BC если диагонали ромба равны 12 и 16.
3) Найдите вектор AC, если A(3;1), C (-1;4)
2.Даны точки A (3;1) , B (-1;4), C (2; -3) D (-2; -4)
1) Найдите координаты и длины векторов AC и BD
2) Найдите координаты и длину вектора m= 3AC-4BD
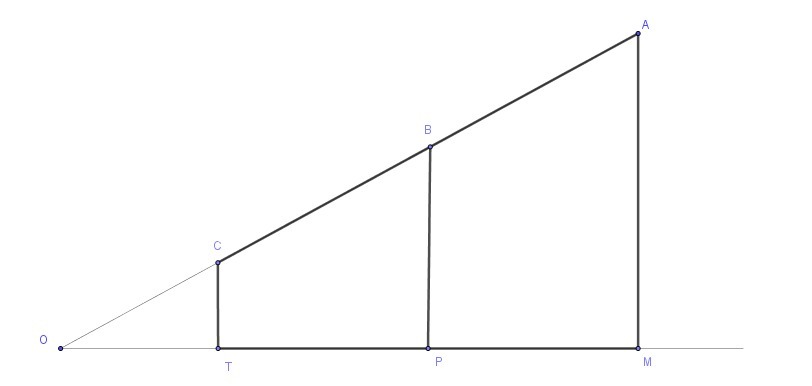
3. Отрезок АС лежит на стороне острого угла О. Из концов отрезка и его середины В опущены перпендикуляры AM, BP и СТ на другую сторону угла. Найдите длину отрезка ВР, если AM = 34 см, СТ = 18 см.
Ответы
Автор ответа:
0
1. Сложение векторов AB + BC определяется из правила параллелограмма.
Путем параллельного переноса соединить начала обоих векторов в одной точке, достроить до параллелограмма. Диагональ параллелограмма является суммой двух векторов
Диагонали в точке пересечения M делятся пополам, т.е.
2) Длину вектора ВС можно найти по теореме Пифагора из прямоугольного треугольника ABM, в нем |BM|=|BD|/2 = 8 см; |AM| = 6 см
см
3) Для начала найдем координаты вектора АС:
2. 1) Координаты вектора АС:
Длина вектора АС: см
2) Координаты вектора BD:
Длина вектора BD: см
3.CT || AM || BP как перпендикулярны к одной прямой, значит четырехугольник AMTC - прямоугольная трапеция, BP - средняя линия трапеции, следовательно
см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Gggggggggggg555555
Предмет: Физика,
автор: karinagroseva02
Предмет: Физика,
автор: anchuk77
Предмет: Химия,
автор: ludarq
Предмет: Математика,
автор: ann03012005