Предмет: Алгебра,
автор: maha89202550420
учитывая три первых члена разложения функций в ряд Макларена,вычислите и определите абсолютную и относительную погрешность вычислений
a)sin*3,14/6
б)е^2
Ответы
Автор ответа:
0
Воспользуемся таблицей "Ряды МаклОрена (не путать с МаклАреном!!!) для элементарных функций" (см. скрин)
Имеем:
eˣ = 1+x+x²/2!+x³/3!+....
e² = 1+2+2²/(1·2)+2³/(1·2·3)+....·
Для четырех слагаемых:
e² = 1+2+2+8/6 ≈ 6,333
Ограничимся ТРЕМЯ слагаемыми:
e² ≈ 1+2+2²/(1·2) = 1+2+2 =5
Ошибка абсолютная
Δx=6,33 - 5 = 1,33
Относительная
ε=Δx/x*100% = 1,33*100%/5 ≈ 27% - колоссальная погрешность.
Вывод - трех первых членов разложения не достаточно!
Для sin (π/6) рассуждения аналогичны, формула разложения - в скрине
Имеем:
eˣ = 1+x+x²/2!+x³/3!+....
e² = 1+2+2²/(1·2)+2³/(1·2·3)+....·
Для четырех слагаемых:
e² = 1+2+2+8/6 ≈ 6,333
Ограничимся ТРЕМЯ слагаемыми:
e² ≈ 1+2+2²/(1·2) = 1+2+2 =5
Ошибка абсолютная
Δx=6,33 - 5 = 1,33
Относительная
ε=Δx/x*100% = 1,33*100%/5 ≈ 27% - колоссальная погрешность.
Вывод - трех первых членов разложения не достаточно!
Для sin (π/6) рассуждения аналогичны, формула разложения - в скрине
Приложения:
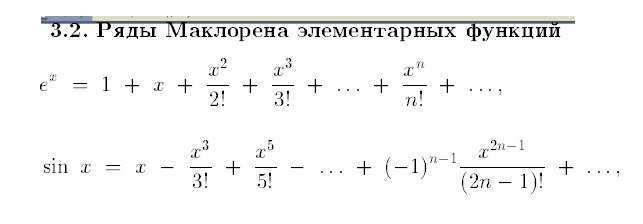
Похожие вопросы
Предмет: Музыка,
автор: gdjdhhd67
Предмет: Музыка,
автор: lubobrosoviclubobros
Предмет: Физика,
автор: Lucsta
Предмет: Математика,
автор: патнрнгр