Предмет: Геометрия,
автор: Denis2001God
Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника
Ответы
Автор ответа:
0
Δ  равносторонний, значит
равносторонний, значит 

Радиус окружности, вписанной в равносторонний треугольник вычисляется по формуле:
 , где
, где  - сторона треугольника
- сторона треугольника

Найдём сторону равностороннего треугольника:





Опустим из вершины B перпендикуляр на сторону AC
 ⊥
⊥ 
 ∩
∩ 


Δ - прямоугольный
- прямоугольный
По теореме Пифагора найдем высоту:

Радиус окружности, вписанной в равносторонний треугольник вычисляется по формуле:
Найдём сторону равностороннего треугольника:
Опустим из вершины B перпендикуляр на сторону AC
Δ
По теореме Пифагора найдем высоту:
Приложения:
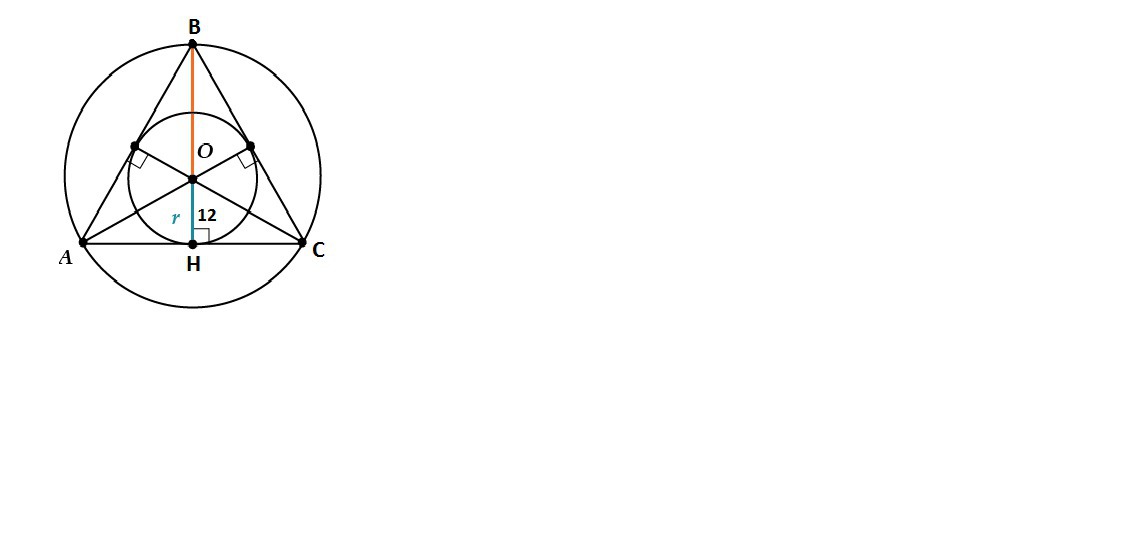
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: smartmobole2
Предмет: Русский язык,
автор: Gdjkn
Предмет: Литература,
автор: Kalinav1
Предмет: Алгебра,
автор: MAfos