Question

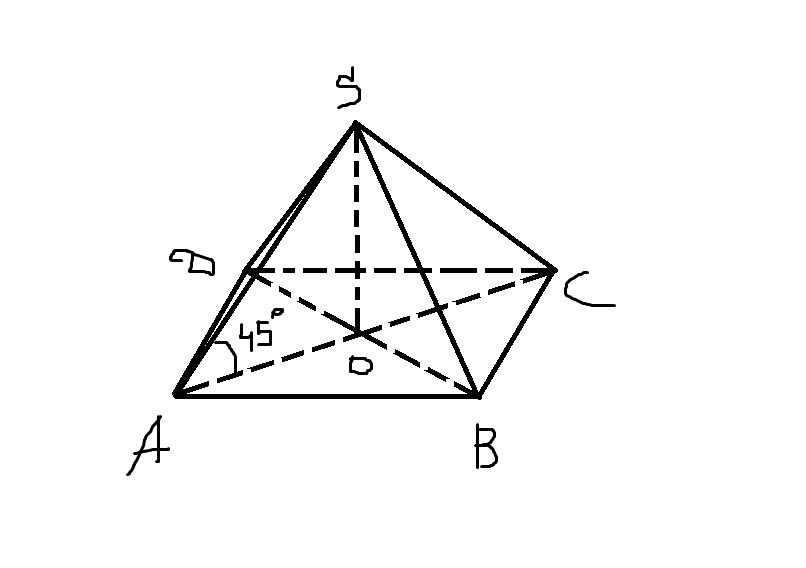
сторона основания правильной четырехугольной пирамиды
равна 2 корня из2 ее боковое ребро наклонено к плоскости под углом 45 вычислите площадь диагонального сечения пирамиды

Answer 1

ABCD-квадрат=>треуг. ACB-прямоуг. Рассмотрим треуг. ACB-прямоуг. По теореме Пифагора AC=корень из AB^2+BC^2=корень из 16=4

AO=OC=AC/2=4/2=2(диагонали квадрата в точке пересечения делятся попалам)

SA-наклонная;AO-проекция;SO-перпендикуляр=>уголSAO=углумежду (SA;(ABC))

Рассм. треуг ASO-прямоуг.

tgSAO=SO/AO

SO=tgSAO*AO=1*2=2

Sasc=1/2*AC*SO=1/2*2*4=4 см^2