Предмет: Алгебра,
автор: yatvoydroug
Логарифмическое неравенство
Заранее огромное спасибо за помощь!
Приложения:
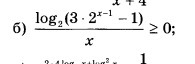
Ответы
Автор ответа:
0
Найдем область определения дроби в левой части. Знаменатель определен при  , числитель определен, если
, числитель определен, если

Заметим, что
Таким образом, область определения дроби

Найдем значения аргумента, при которых числитель неотрицателен:


Таким образом, на интервале и числитель и знаменатель принимают отрицательные значения, поэтому дробь принимает положительные значения и все точки этого интервала нам подойдут.
и числитель и знаменатель принимают отрицательные значения, поэтому дробь принимает положительные значения и все точки этого интервала нам подойдут.
На интервале числитель принимает отрицательные значения, а знаменатель принимает положительные значения, поэтому дробь принимает отрицательные значения.
числитель принимает отрицательные значения, а знаменатель принимает положительные значения, поэтому дробь принимает отрицательные значения.
На луче числитель принимает неотрицательные значения, знаменатель принимает положительные значения, поэтому дробь принимает неотрицательные значения и все точки этого луча нам подойдут.
числитель принимает неотрицательные значения, знаменатель принимает положительные значения, поэтому дробь принимает неотрицательные значения и все точки этого луча нам подойдут.
Ответ:
Заметим, что
Таким образом, область определения дроби
Найдем значения аргумента, при которых числитель неотрицателен:
Таким образом, на интервале
На интервале
На луче
Ответ:
Автор ответа:
0
Боже мой, спасибо ВАМ ОГРОМНОЕ! Тысячу раз спасибо!
Похожие вопросы
Предмет: Алгебра,
автор: jokermase4
Предмет: История,
автор: Leralera1234lera
Предмет: Литература,
автор: vasadolinnij
Предмет: Алгебра,
автор: angel240501
Предмет: Литература,
автор: emilemil2626