Предмет: Математика,
автор: angelina11volkova
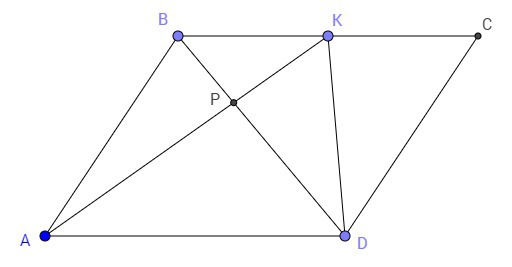
На стороне BC параллелограмма ABCD выбрана точка K. Отрезки AK и BD пересекаются в точке P. Площадь параллелограмма ABCD равна 24, а площадь четырёхугольника PKCD равна 10. Найдите площадь треугольника APD.(можно чертеж и решение?)
Ответы
Автор ответа:
0
Параллелограмм делится диагональю на два равных треугольника.
S△ABD = S△BCD = 24/2 = 12
S△BKP = S△BCD - S PKCD = 12-10 = 2
Треугольники, лежащие на боковых сторонах трапеции при пересечении диагоналей, равновеликие.
S△ABP = S△KDP = x
S△BKD = S△KDP + S△BKP = x+2
Если два треугольника имеют общий угол, то их площади относятся как произведения сторон, заключающих этот угол.
△ABP и △ABD:
BP·AB / BD·AB = x/12 <=> BP/BD = x/12
△BKP и △BKD:
BP·BK / BD·BK = 2/(x+2) <=> BP/BD = 2/(x+2)
x/12 = 2/(x+2) <=> x(x+2) = 24 <=> x^2 +2x -24 = 0
x(1,2) = -1±√(1+24) = -1±5
x1= -6 (x>0)
x2= 4
S△APD = S△ABD - S△ABP = 12-4 = 8
S△ABD = S△BCD = 24/2 = 12
S△BKP = S△BCD - S PKCD = 12-10 = 2
Треугольники, лежащие на боковых сторонах трапеции при пересечении диагоналей, равновеликие.
S△ABP = S△KDP = x
S△BKD = S△KDP + S△BKP = x+2
Если два треугольника имеют общий угол, то их площади относятся как произведения сторон, заключающих этот угол.
△ABP и △ABD:
BP·AB / BD·AB = x/12 <=> BP/BD = x/12
△BKP и △BKD:
BP·BK / BD·BK = 2/(x+2) <=> BP/BD = 2/(x+2)
x/12 = 2/(x+2) <=> x(x+2) = 24 <=> x^2 +2x -24 = 0
x(1,2) = -1±√(1+24) = -1±5
x1= -6 (x>0)
x2= 4
S△APD = S△ABD - S△ABP = 12-4 = 8
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Nikki865
Предмет: Геометрия,
автор: llppnmr
Предмет: Биология,
автор: irunika
Предмет: Математика,
автор: FunexSchool
Предмет: Химия,
автор: 6684328