Предмет: Алгебра,
автор: vosmiklassnik
Необходимо найти производную функций. Прошу помочь!
Приложения:
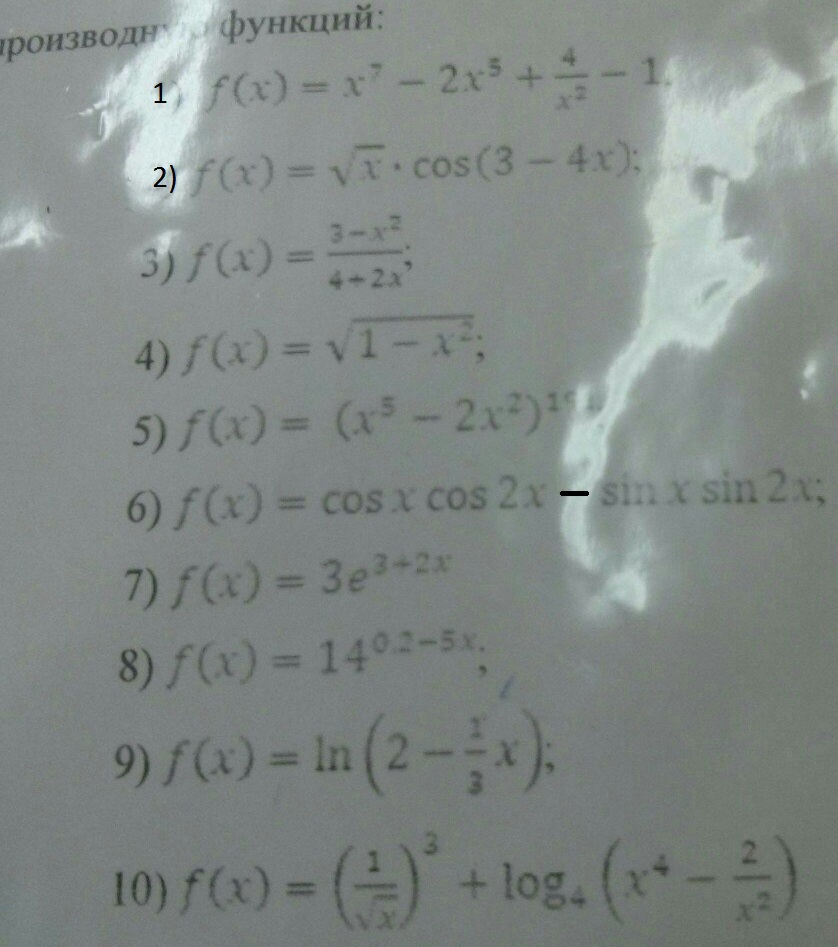
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Қазақ тiлi,
автор: medinauakhit
Предмет: Қазақ тiлi,
автор: elvirabatyrova73
Предмет: Геометрия,
автор: PowerInspire
Предмет: Биология,
автор: vikatsar1998