Предмет: Геометрия,
автор: alexeewna01
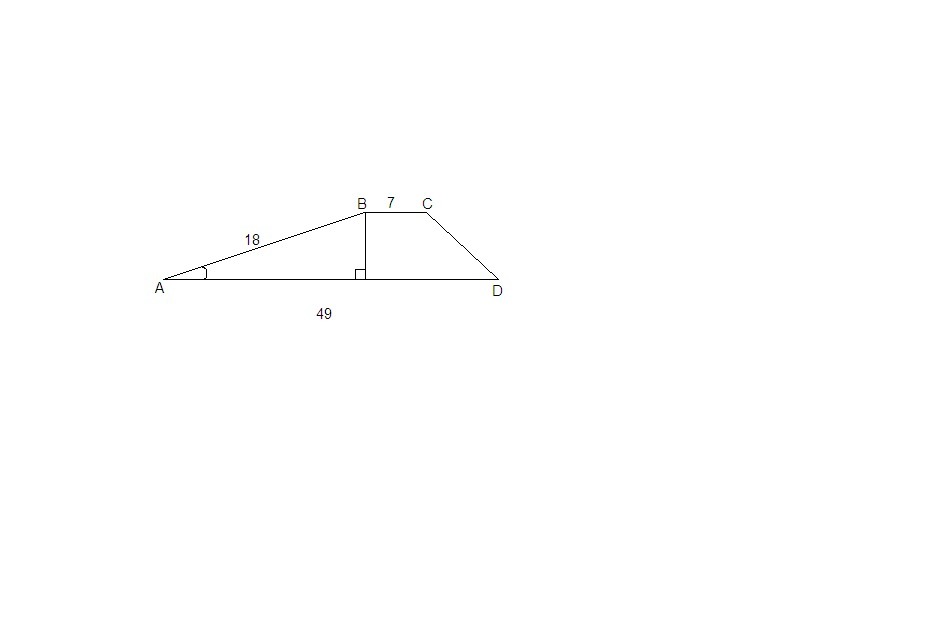
Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен Найдите площадь трапеции.
Ответы
Автор ответа:
0
Исправленное условие: Основания
трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла
между ней и одним из оснований равен 2√10/7. Найдите площадь трапеции.
Косинус угла между боковой стороной и основанием положительный, значит это острый угол.
sin∠A = √(1 - cos²∠A) = √(1 - 40/49) = √(9/49) = 3/7
Проведем высоту ВН.
ΔАВН: ∠АНВ = 90°
sin∠BAH = BH/AB
BH = AB · sin∠A = 18 · 3/7 = 54/7
Sabcd = (AD + BC)/2 · BH
Sabcd = (49 + 7)/2 · 54/7 = 56/2 · 54/7 = 8 · 27 = 216
Косинус угла между боковой стороной и основанием положительный, значит это острый угол.
sin∠A = √(1 - cos²∠A) = √(1 - 40/49) = √(9/49) = 3/7
Проведем высоту ВН.
ΔАВН: ∠АНВ = 90°
sin∠BAH = BH/AB
BH = AB · sin∠A = 18 · 3/7 = 54/7
Sabcd = (AD + BC)/2 · BH
Sabcd = (49 + 7)/2 · 54/7 = 56/2 · 54/7 = 8 · 27 = 216
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: habirovailona6
Предмет: Русский язык,
автор: uumit2662
Предмет: Математика,
автор: myrzabekovaaruzan0
Предмет: Математика,
автор: sergloban94