Предмет: Геометрия,
автор: natar2030
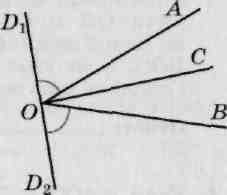
Через вершину угла АОВ проведена прямая D1D2 так, что ∟ AOD1 = ∟BOD2 = 70°. Найдите угол между прямой D1D2 и прямой, содержащей биссектрису ОС данного угла. Помогите срочноо!!
Приложения:
Ответы
Автор ответа:
0
Ответ:
<COD1 = <COD2 =90°
Объяснение:
Угол между прямой D1D2 и прямой, содержащей биссектрису ОС угла АОВ - это угол COD1 или смежный с ним угол COD2.
∠D1D2 - развернутый угол и равен 180°. Следовательно,
<AOB = 180° - 2*70° = 40°.
Биссектриса ОС угла ∠АОВ делит его пополам. =>
∠AOC = ∠BOC = 20°.
∠D1OC = ∠AOD1+∠АОС = 70°+20° = 90°.
∠D2OC = ∠BOD2+∠BOC = 70°+20° = 90°.
Похожие вопросы
Предмет: Литература,
автор: zhaziraelaman0505
Предмет: История,
автор: Nargizok2020
Предмет: Қазақ тiлi,
автор: simkona2010
Предмет: Информатика,
автор: tanyushka991
Предмет: Алгебра,
автор: madrave787