Предмет: Алгебра,
автор: kzede
№16 Решить систему уравнений
Приложения:

Ответы
Автор ответа:
0
Ответ: {(6;8),(8;6)}
Приложения:
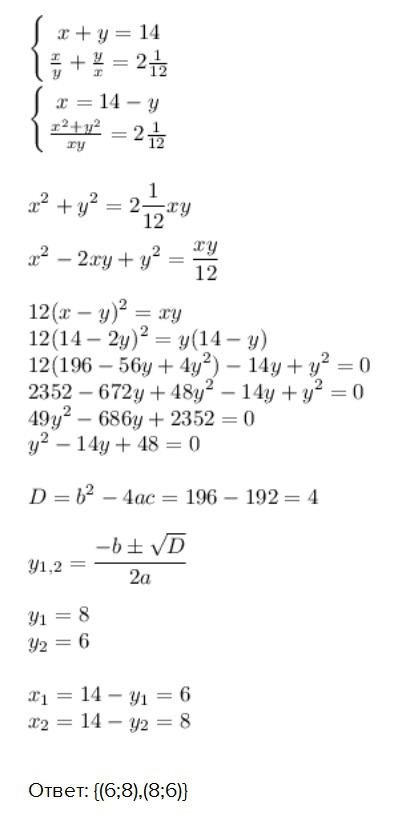
Похожие вопросы
Предмет: Физика,
автор: napoleonekieffer
Предмет: Українська література,
автор: valeriaivanusa
Предмет: Немецкий язык,
автор: sas19876068
Предмет: Физика,
автор: berdibekaida060