Предмет: Алгебра,
автор: Харли2000
Докажите
tg1 * tg2*tg3*......tg88*tg89=1
* это умножение
Нужно правильно и срочно даю 30 баллов
Ответы
Автор ответа:
0
Решение смотри в приложении
Приложения:
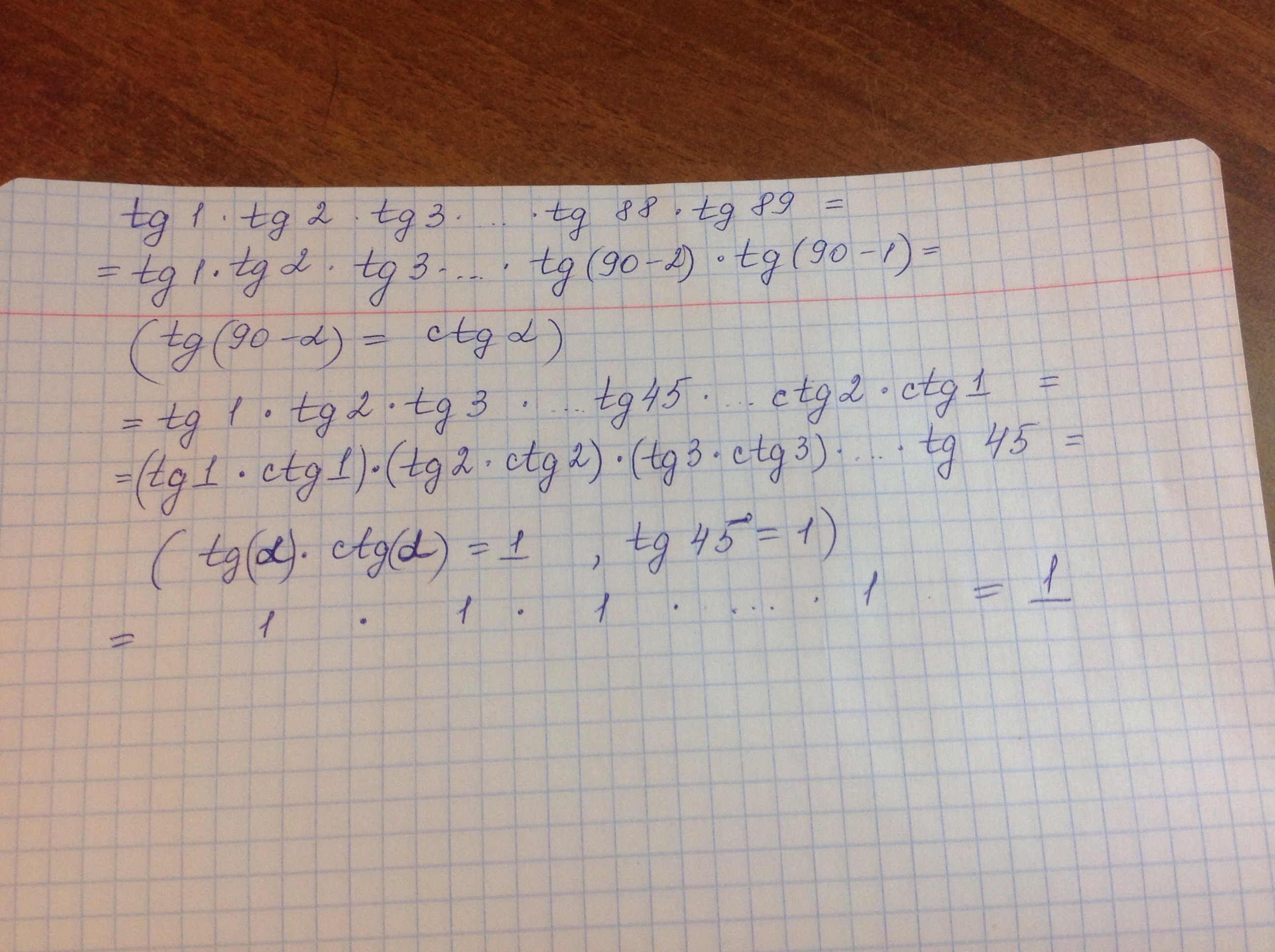
Автор ответа:
0
вау спс
Автор ответа:
0
Что и требовалось доказать.
Примечание:
Т.е. составляем произведения первого и последнего, второго и предпоследнего и т.д. Остаётся лишь tg45=1
В левой части уравнения - произведения единиц, равные 1. Правая часть уравнения также равна единице. Тождество доказано.
Приложения:
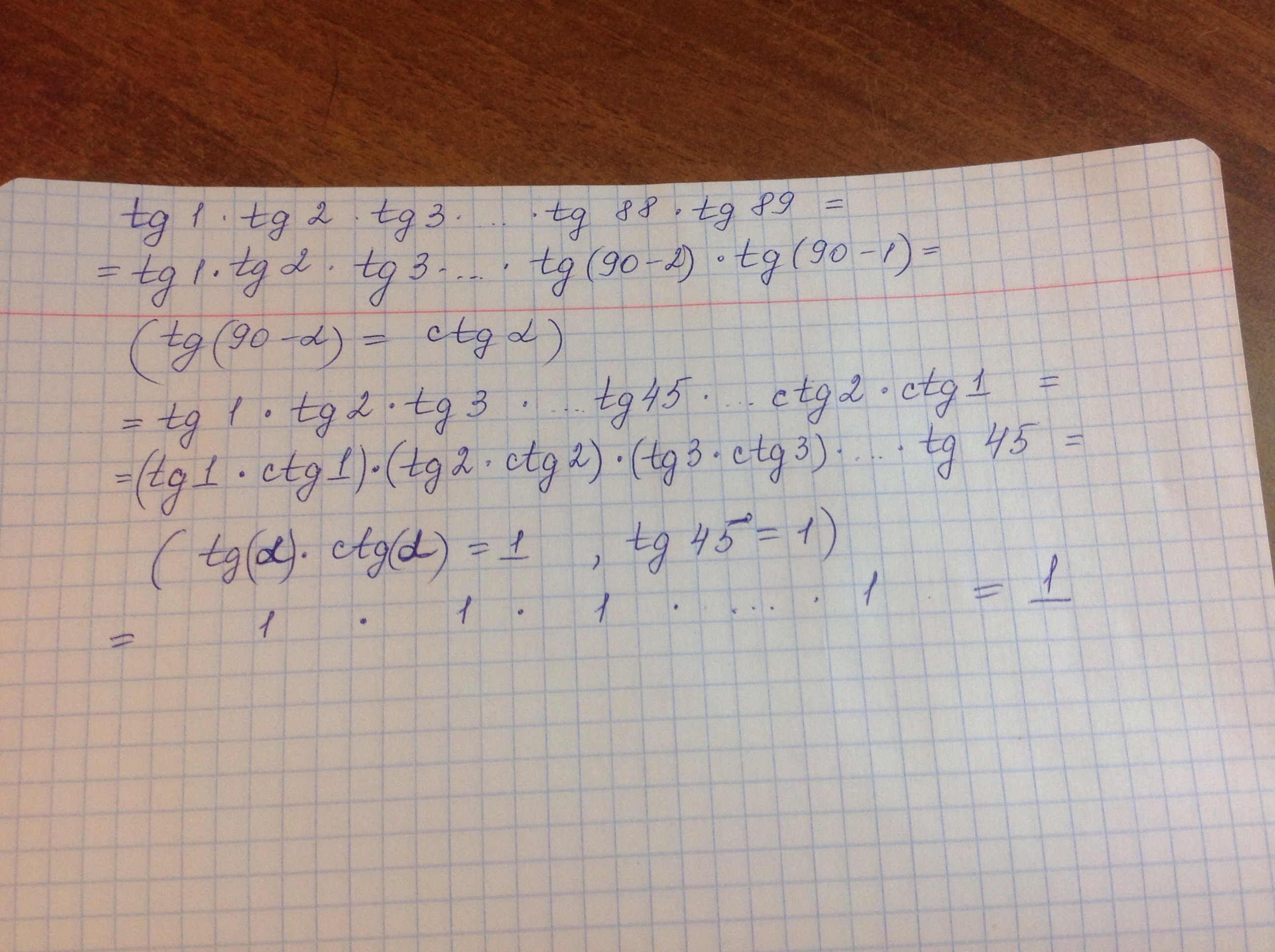
Похожие вопросы
Предмет: Математика,
автор: artemamidov755
Предмет: Биология,
автор: uglyovsa
Предмет: География,
автор: mitrovavlada
Предмет: Математика,
автор: marinаpa
Предмет: Математика,
автор: nadjahleba