Предмет: Алгебра,
автор: respoison
Помогите пожалуйста!
Приложения:
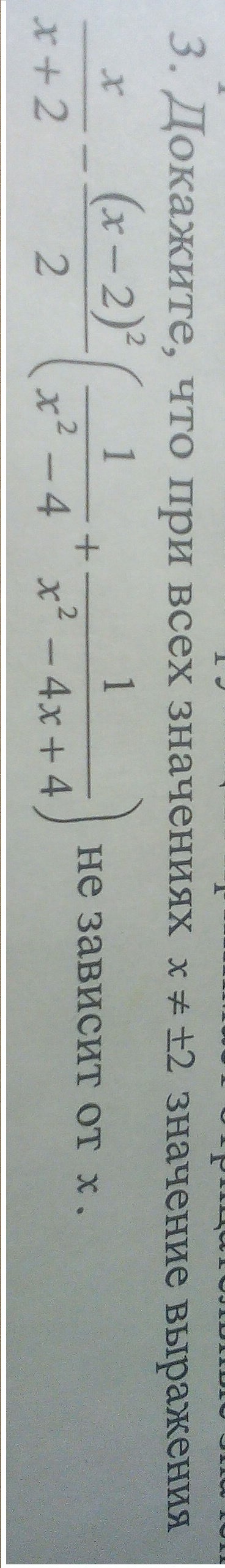
Ответы
Автор ответа:
0
x/(x+2)-[(x-2)²/2]·[1/(x²-4)+1/(x²-4x+4)]=
=x/(x+2)-[(x-2)²/2]·[1/((x-2)(x+2))+1/(x-2)²]=
=x/(x+2)-[(x-2)²/2]·[(x-2)/((x-2)²(x+2))+(x+2)/((x-2)²(x+2))]=
=x/(x+2)-[(x-2)²/2]·[((x-2)+(x+2))/((x-2)²(x+2))]=
=x/(x+2)-[(x-2)²/2]·[2x/((x-2)²(x+2))]=x/(x+2)-x/(x+2)=0
т.о x/(x+2)-[(x-2)²/2]·[1/(x²-4)+1/(x²-4x+4)] не зависит от х
=x/(x+2)-[(x-2)²/2]·[1/((x-2)(x+2))+1/(x-2)²]=
=x/(x+2)-[(x-2)²/2]·[(x-2)/((x-2)²(x+2))+(x+2)/((x-2)²(x+2))]=
=x/(x+2)-[(x-2)²/2]·[((x-2)+(x+2))/((x-2)²(x+2))]=
=x/(x+2)-[(x-2)²/2]·[2x/((x-2)²(x+2))]=x/(x+2)-x/(x+2)=0
т.о x/(x+2)-[(x-2)²/2]·[1/(x²-4)+1/(x²-4x+4)] не зависит от х
Похожие вопросы
Предмет: Английский язык,
автор: eva9824
Предмет: Математика,
автор: vikt0riacloudy
Предмет: История,
автор: Cobaka12345689000000
Предмет: Математика,
автор: sofi2000q